Разбиением натурального числа n на k слагаемых называется последовательность таких положительных натуральных чисел ( a₁, a₂, …, a_k ), что

n = a₁ + a₂ + …+ a_k,               k > 0,                        a₁³  a₂³ …³  a_k  > 0.

Пусть P(n,k) – число разбиений n на k слагаемых. Тогда число всех разбиений равно:

,     n>0.

Полагаем по определению P(0) = P(0,0) = 1.

Пример 1

P(5) = 7:

5 = 5,

5 = 4 + 1;

5 = 3 + 2;

5 = 3 + 1 + 1;

5 = 2 + 2 + 1;

5 = 2 + 1 + 1 + 1;

5 = 1 + 1 + 1 + 1 + 1.

Замечание

Каждое разбиение можно наглядно представить с помощью диаграммы Ферреса, которая для n = a₁ + a₂ + …+ a_k состоит из k строк, а i-строка содержит a_i точек. Например, для 5 = 2 + 2 + 1 диаграмма Ферреса имеет вид (рис. 3.1, а). Если отразить диаграмму относительно ее главной диагонали, то мы получим  диаграмму Ферреса, которая называется сопряженной (рис. 3.1, б). Она будет соответствовать разбиению 5 = 3 + 2.

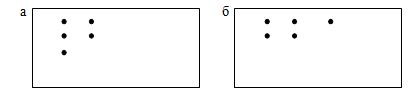
Рис. 3.1. Диаграммы Ферреса

Лемма 1

Число разбиений P(n) равно количеству решений

(l₁, l₂, …, l_n )

уравнения  l₁ ×1 + l₂ ×2 + …+ l_n               ×n = n.

Доказательство

Если среди чисел a₁ ³ a₂ ³ …³ a_k  разбиения числа n имеется l₁ единиц, l₂ двоек,   …, l_n   — n-ок, то получаем решение уравнения. Ясно, что это соответствие взаимно однозначно.

Обозначим через P_h(n) количество разбиений числа n на слагаемые, не большие чем h.

Теорема 1

Производящая функция последовательности чисел разбиений P_h(0), P_h (1), P_h (2), … равна:

.

Доказательство

Произведение равно:

(1  +x + x² +…)(1 + x² + x⁴ +…)(1 + x³ + x⁶+ …)×… (1 + x^h + x^2h + …).

Если перемножить содержимое скобок, то получим многочлен, равный сумме одночленов . Отсюда коэффициент при xⁿ равен числу последовательностей (l₁, l₂, …×, l_h), для которых   l₁ ×1 + l₂ ×2 + …+ l_h ×h = n. Он будет равен числу разбиений n на слагаемые, не большие чем h.

Следствие 1

Производящая функция последовательности чисел разбиений  P(0), P(1), P(2),… равна:

.