Рассмотрим сначала преобразование поворота в плоскости Oxy на угол J вокруг точки (x₀,y₀). Переходя к полярным координатам с центром в (x₀,y₀), запишем                x-x₀=rcosf, y-y₀=rsinf, где r — расстояние между точками (x,y) и (x₀,y₀), а f — некоторый угол. После поворота на угол J точка (x,y) перейдет в точку `x=x<sub>0</sub>+rcos(f+J), `y=y₀+rsin(f+J). Отсюда

`x=x₀+(x-x₀)cosJ-(y-y₀)sinJ,

`y=y₀+(x-x₀)sinJ +(y-y₀)cosJ.

В частности, при x₀=0, y₀=0 вектор (x,y) умножается на матрицу

При J=p/2 получаем

Пусть теперь задана декартова система координат в трехмерном пространстве. Требуется вычислить коэффициенты матрицы вращения вокруг единичного вектора u на угол J. Рассмотрим произвольную точку, имеющую радиус-вектор r. Проекция вектора r на ось, проходящую через вектор u, не изменится после поворота, значит, если r’ — образ вектора r, то (r×u)u=(r’×u)u. Проекция на перпендикулярную вектору u плоскость равна r-(r×u)u. Выберем в плоскости, перпендикулярной вектору u, произвольную декартову систему координат, заданную с помощью пары ортогональных единичных векторов u₁ и u₂. Пусть вектор r-(r×u)u в этой системе координат имеет координаты (x,y). Тогда r-(r×u)u=xu₁+yu₂. После поворота на угол J вектор r перейдет в такой вектор r’, что

r’-(r×u)u=(xcosJ-ysinJ)u₁+(xsinJ+ycosJ)u₂=cosJ (xu₁+yu₂)+sinJ (-yu₁+xu₂).

Вектор -yu₁+xu₂ получается из вектора xu₁+yu₂ поворотом на угол p/2 вокруг оси u, поэтому

-yu₁+xu₂=u´(xu₁+yu₂)=u´(r-(r×u)u)=u´r.

Следовательно,

r’=(r×u)u+cosJ(r-(r×u)u)+sinJ(u´r).

Учитывая, что в матричной форме (r×u)u=(u^Tr)u=u(u^Tr)=uu^Tr, где u^T — матрица, состоящая из одной строки (u_x,u_y,u_z),

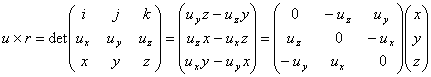
получаем матрицу вращения вокруг вектора u=(u_x,u_y,u_z). Пусть Id — единичная матрица. Тогда матрица вращения будет равна

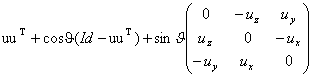
Если перейти к другой системе координат, то преобразование вращения в новой системе координат изменится. Более того, при переходе к координатам в пространстве изображения для центральной проекции вращение уже не будет линейным преобразованием. Пусть координаты вектора v=(x,y,z) выражаются через новые координаты v’=(x’,y’,z’) как v=S(v’). Рассмотрим произвольное преобразование F:R³®R³. Тогда если w=F(v) и w’ – новые координаты точки w, то S(w’)=F(S(v’)). Если преобразование S замены координат имеет обратное преобразование S^-1, то w’=S^-1°F°S(v’). (Здесь ‘°‘ обозначает композицию преобразований). В частности, для того чтобы получить координаты точки в пространстве изображения, надо применить к этой точке сначала преобразование, обратное к видовому, затем полученные координаты помножить на матрицу вращения и далее применить видовое преобразование. (Видовое преобразование было описано в пп. 3.1.)