Определение. Граф G называется деревом, если он является связным и не имеет циклов. Граф G, все компоненты связности которого являются деревьями, называется лесом.
Пример 86.
Граф G1 является деревом (рис. 3.20). Граф G2 является лесом (рис. 38), он содержит три связные компоненты, каждая из которых является деревом.
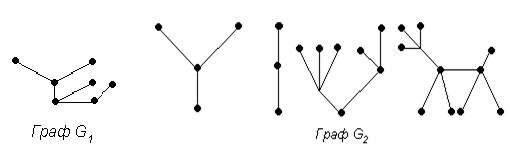
Рис. 3.20. Пример дерева и леса
Следующие утверждения эквивалентны:
а) граф G есть дерево;
б) граф G является связным и не имеет простых циклов;
в) граф G является связным и число его ребер ровно на единицу меньше числа вершин;
г) любые две различные вершины графа G можно соединить единственной (и притом простой) цепью;
д) граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один (с точностью до направления обхода и начальной вершины обхода) и притом простой цикл (проходящий через добавляемое ребро).
Утверждение. Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдется висячая вершина.
Утверждение. Пусть G – дерево. Тогда любая цепь в G будет простой.