Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начинает колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При распространении колебаний не учитывается дискретное строение среды, и среда рассматривается как сплошная, т.е. непрерывно распределенная в пространстве и обладающая упругими свойствами.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от природы, является перенос энергии без переноса вещества.
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространению волны.
 Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т.е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т.е. твердых телах. В жидкостях и газах возникают только продольные волны, а в твердых телах – как продольные, так и поперечные.
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т.е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т.е. твердых телах. В жидкостях и газах возникают только продольные волны, а в твердых телах – как продольные, так и поперечные.
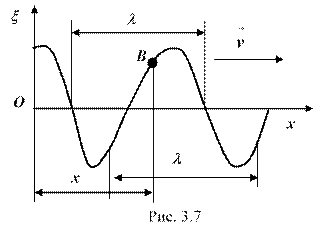
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис. 3.7 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т.е. приведена зависимость между смещением (x) частиц среды, участвующих в волновом процессе, и расстоянием (х) этих частиц (например частицы А) от источника колебаний О для какого-то фиксированного момента времени t. Приведенный график функции x(х, t) похож на график гармонического колебания, однако они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний – зависимость смещения данной частицы от времени.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны (l). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период:
![]() ,
,
или, учитывая, что ![]() , где
, где ![]() – частота колебаний,
– частота колебаний,
![]() .
.
Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, а колеблется совокупность частиц, расположенных в некотором объеме, т.е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называются волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновой фронт также является волновой поверхностью. Волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.