Определение. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G) – 1 ребер. Таким образом, любое остовное дерево графа G есть результат удаления из G ровно m(G)-(n(G)-1)=m(G)-n(G)+1 ребер.

Определение. Число m(G)-n(G)+1 называется цикломатическим числом связного графа G и обозначается через v(G).

Замечание.  Понятие остовного дерева и цикломатического числа аналогичным образом определяется и для произвольного связного псевдографа G.

Покажем существование остовного дерева для произвольного связного псевдографа G=(V,X), описав алгоритм его выделения.

Шаг 1. Выбираем в G произвольную вершину u₁, которая образует подграф G₁ псевдографа G, являющийся деревом. Полагаем i=1.

Шаг 2. Если i=n, где n=n(G), то задача решена, и G_i – искомое остовное дерево псевдографа G. В противном случае переходим к шагу 3.

Шаг 3. Пусть уже построено дерево G_i, являющееся подграфом псевдографа G и содержащее некоторые вершины  u₁, …, u_i, где 1≤i≤n-1. Строим граф G_i+1, добавляя к графу G_i новую вершину u_i+1 V, смежную в G с некоторой вершиной u_j графа G_i, и новое ребро (u_i+1, u_j) (в силу связности G и того обстоятельства, что i < n, указанная вершина u_i+1 обязательно найдется). Согласно утверждению граф G_i+1 также является деревом. Присваиваем i:=i+1 и переходим к шагу 2.

Пример 87.

Используя алгоритм, выделим остовное дерево графа G, изображенного на рис. 39.

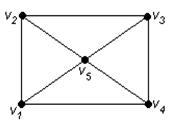
Рис. 3.21. Граф для примера 87

Решение.

На рис. 3.22 приведена последовательность графов G_i, i=1, 2, 3, 4, 5, получаемых в результате выполнения алгоритма.

При этом в силу того, что n(G)=5, G₅ — остовное дерево графа G.

Замечание. Остовное дерево связного графа может быть выделено, вообще говоря, не единственным способом.

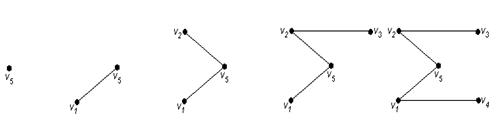
Рис. 3.22. Последовательность графа в результате выполнения алгоритма для примера 87

Общее число остовных деревьев связного графа может оказаться весьма большим. Например, для полного графа с n вершинами оно равно n^n-2.

В общем случае обозначим через G произвольный граф с n вершинами, m ребрами и k компонентами. Как уже было сказано, применяя выше описанный алгоритм, получим в результате граф, являющийся остовным лесом.

Определение. Число ребер, удаленных при построении остовного леса произвольного графа G, называется цикломатическим числом (или цикломатическим рангом) графа G и обозначается через g (G) = m – n + k.

Пример 88.

Циклический ранг дерева равен нулю, а циклический ранг циклического графа равен единице.

Определение. Коциклическим рангом графа G называется число ребер в его остовном дереве.

С понятием остовного леса Т графа G тесно связано понятие фундаментальной системы циклов, ассоциированной с Т.

Определение. Если добавить к Т любое не содержащиеся в нем ребро графа G, то получим единственный цикл; множество всех циклов, получаемых таким способом (т.е. путем добавления по отдельности каждого ребра из G, не содержащегося в Т), называется фундаментальной системой циклов, ассоциированной с Т.