Если в некоторой среде распространяется плоская продольная волна, то этот элемент среды массой ![]() =
=![]() обладает кинетической энергией:
обладает кинетической энергией:
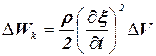 ,
,
где ![]() – скорость элемента.
– скорость элемента.
Потенциальная энергия упругой деформации объемом ![]() имеет вид:
имеет вид:
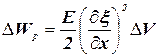 ,
,
где ![]() – модуль Юнга среды.
– модуль Юнга среды.
Тогда полная энергия с учетом (3.15) и (3.16) запишется в виде:
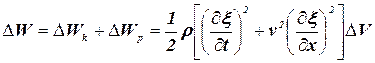 .
.
Разделив эту энергию на объем ![]() , в котором она содержится, получим плотность энергии:
, в котором она содержится, получим плотность энергии:
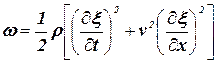 .
.
Количество энергии dW, переносимое волной через некоторую поверхность в единицу времени dt, называется потоком энергии (Ф) через эту поверхность:
![]() .
.
Поток энергии в различных точках среды может быть различной интенсивности. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии(j) (вектор Умова):
![]()
или
![]() ,
,
где ![]() – площадка поверхности; w – плотность энергии; v – фазовая скорость волны.
– площадка поверхности; w – плотность энергии; v – фазовая скорость волны.