Вычислим производящую функцию F(x) чисел Фибоначчи:
F0 = F1 = 1, Fn+1 = Fn + Fn-1 при n ³ 1.
Таким образом, числа Фибоначчи – это последовательность чисел 1, 1, 2, 3, 5… Имеют место соотношения:
![]() .
.
Приходим к уравнению:
F(x) = 1 + x + x2 + x(F(x) – 1)
для ![]() .
.
Решая это уравнение, получаем:
![]() ,
,
для некоторых A, B, при ![]() ,
, ![]() .
.
Отсюда мы видим, что ряд F(x) равен сумме геометрических прогрессий. Находим:
![]() ,
, ![]() .
.
Следовательно,
![]() .
.
Отсюда получаем формулу для вычисления k-го числа Фибоначчи:
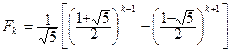 ,
,
для всех k = 0, 1, 2, …