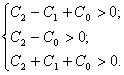Билинейное преобразование:

  и                                                       (3.1)

переводит точки единичной окружности на плоскости z в точки, лежащие на мнимой оси плоскости w, и наоборот. Любой точке, распложенной внутри этой окружности, согласно выражению (3.1) соответствует точка левой полуплоскости w, а точки, находящиеся вне окружности, отображаются в точки, принадлежащие правой полуплоскости w.

Следовательно, условие устойчивости дискретной САУ, связанное с принадлежностью z-корней характеристического уравнения  единичному кругу, равносильно условию принадлежности левой w-полуплоскости корней уравнения , полученного из исходного уравнения путем билинейного преобразования (3.1).

Решение такой задачи может быть осуществлено с использованием известных критериев, разработанных для оценки устойчивости непрерывных систем, например критериев Рауса или Гурвица.

Пример 20

Необходимо оценить устойчивость замкнутой дискретной системы второго порядка, характеристическое уравнение которой в общем случае записывается в виде:

.

Используя билинейное преобразование (3.1), осуществляем переход к переменной w:

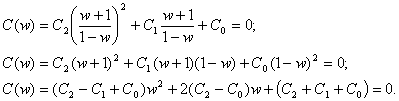
Согласно критерию Гурвица необходимым и достаточным условием устойчивости замкнутой САУ является положительность коэффициентов ее характеристического

уравнения. Следовательно, условие устойчивости рассматриваемой дискретной системы: