1. На первом шаге прямого хода метода Гаусса выбирается максимальный по модулю элемент в первом столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом 
, то перестановкой строк помещаем его в . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.
2. На 
-м шаге прямого хода метода Гаусса непреобразованный столбец – это часть столбца i, начиная с элемента 
, то есть 
. Находим максимальный по модулю элемент в непреобразованном столбце. Этот элемент является ведущим. Если он равен нулю, то detA = 0. Если ведущий элемент не является элементом , то перестановкой строк помещаем его в . При этом соответственно переставляются элементы вектора b. Затем применяются формулы метода Гаусса.
3. После (n-1)-го шага получаем верхнюю треугольную матрицу U и преобразованный вектор правой части. Выполняем обратную подстановку.
Метод Гаусса с частичным выбором ведущего элемента в отсутствие ошибок округления для невырожденных матриц позволяет получить точное решение, а для вырожденных матриц – сообщение о том, что матрица вырождена.
Пример
Решить систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента.
Решение
Рассмотрим ту же систему линейных уравнений, что и в предыдущих примерах.
Прямой ход метода Гаусса
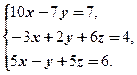
Прежде всего, выбираем максимальный по модулю элемент в первом непреобразованном столбце:
, 
, следовательно, ведущим элементом является 10.
Ведущим элементом является элемент , поэтому перестановка строк не нужна. Умножим первое уравнение на 0.3 и прибавим ко второму. Умножим первое уравнение на -0.5 и прибавим к третьему. Получим:
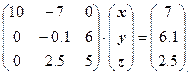
Рассмотрим следующий непреобразованный столбец:
, 
, следовательно, ведущим элементом является 2.5, а не -0.1, как в методе Гаусса без выбора ведущего элемента. Но ведущий элемент не является элементом 
(
при 
) , поэтому необходимо переставить строки матрицы А, чтобы элемент 2.5 стал элементом . При перестановке строк необходимо одновременно поменять местами элементы вектора правой части 
. Получим:
.
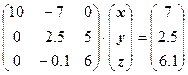Умножим второе уравнение на 0.4 и прибавим к третьему. Получим:
.
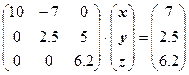Мы получили систему линейных уравнений с верхней треугольной матрицей.
Обратная подстановка
, следовательно, 
;
, 
;
, 
Ведущими элементами являются числа: 10, 2.5, 6.2, все они по модулю больше 1, следовательно, алгоритм является вычислительно устойчивым.
В методе Гаусса с частичным выбором ведущего элемента, в отличие от метода Гаусса без выбора ведущего элемента, в случае необходимости меняются местами уравнения системы линейных уравнений. За счет этого не возникает проблем, если у невырожденной матрицы какой-либо из главных миноров равен нулю.
Рассмотрим метод Гаусса с частичным выбором ведущего элемента с точки зрения операций над матрицами.
Теорема
Произвольная невырожденная матрица перестановкой строк (столбцов) может быть приведена к матрице с главными минорами, отличными от нуля (
, где P – матрица перестановок).
Матрица Р получается из единичной матрицы перестановкой строк (столбцов).
Сложность метода Гаусса с частичным выбором ведущего элемента
Число арифметических действий, необходимых для его реализации: 
, где n – число уравнений. Оценим сложность по памяти: требуется память для хранения n2 элементов матрицы, вектора b (n элементов) и вектора x (n элементов), в результате, 
.
Метод Гаусса с частичным выбором ведущего элемента является устойчивым, если все ведущие элементы по модулю больше единицы.
Следует отметить, что метод Гаусса с частичным выбором ведущего элемента – это основной алгоритм вычислительной математики линейной алгебры.
Метод Гаусса с полным выбором ведущего элемента отличается от метода Гаусса с частичным выбором ведущего элемента тем, что на каждом шаге прямого хода ведущий элемент ищется в непреобразованной части матрицы. Непреобразованная часть матрицы – это квадратная матрица размерности n-i+1, получаемая вычеркиванием первых i – 1 строк и первых i – 1 столбцов. В методе Гаусса с полным выбором ведущего элемента возможна не только перестановка строк матрицы и соответствующих элементов правой части, но и перестановка столбцов матрицы и, соответственно, изменение порядка следования неизвестных.