Как уже указывалось, модели на метауровне характеризуются большим разнообразием типов, они моделируют системы, описываемые математической теорией массового обслуживания (ТМО), к ним относятся имитационные модели и ряд других.
Характеристики и параметры статистической совокупности
В результате непосредственных наблюдений, измерений или регистрации фактов получается множество данных, которые образуют статистическую совокупность и нуждаются в обработке, включающей систематизацию и классификацию, расчетов параметров, характеризующих эту совокупность, а также составление таблиц, графиков, гистограмм, иллюстрирующих процесс.
Основным этапом обработки экспериментальных данных является группировка, то есть разделение статистической совокупности на группы, однородные по какому-то признаку. Благодаря группировке собранный материал приобретает систематизированный вид, поэтому выделение тех или иных групп должно быть не формальным, а обоснованным исходя из целей исследования.
Наиболее полную характеристику статистической совокупности дает функция распределения вероятностей случайной величины. Однако на практике часто используют ограниченное количество числовых характеристик, называемых параметрами распределения. Их можно разделить на три класса, которые характеризуют:
- центр группирования (среднее арифметическое – в MathCADе функция mean(x));
- величину рассеяния (степень вариации);
- форму распределения вероятностей.
Самой элементарной характеристикой рассеяния является вариационный размах, представляющий собой разность между максимальным и минимальным значениями статистической совокупности:
. (3.11)
Вариационный размах не всегда характерен, так как учитывает только крайние значения, которые могут очень сильно отличаться от всех других значений. Более точно рассеяние определяется с помощью показателей, учитывающих отклонение всех значений от среднего арифметического, то есть среднее линейное и среднее квадратичное отклонения. Среднее линейное определяется по формуле:
. (3.12)
Среднее квадратичное отклонение вычисляется по формуле:
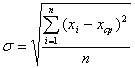. (3.13)
Величина под корнем называется дисперсией. Она имеет самостоятельное значение во многих задачах математической статистики и относится к числу важнейших показателей вариации.
В качестве математических моделей статистических распределений используются теоретические кривые распределения. Теоретическая кривая – это зависимость, которая описывается математически, то есть может быть выражена уравнением с определенными параметрами. Известно очень много различных распределений, однако на практике используются лишь некоторые из них.
При расчете надежности аппаратуры, анализе точности и проверке стабильности, а также при проверке эффективности усовершенствований и имитационном моделировании производственных процессов на ЭВМ наиболее часто используются следующие распределения:
- равномерное распределение – это равновероятное распределение, то есть любому значению случайной переменной соответствует одна и та же вероятность (рис. 3.9). В природе редко встречаются физические явления с равномерным распределением. Тем не менее такое распределение используется всегда, когда имеет место чисто случайный выбор между несколькими альтернативами. Если о законе распределения проектировщику ничего не известно, его принимают равновероятностным. В системе MathCAD имеются две функции равномерного распределения вероятности – rnd(x) и runif(m,a,b). Приведем пример:
Равномерное распределение:
Число случайных чисел: m:=100.
Генерируемый диапазон чисел: а:=0; b:=4.
Число интервалов гистограммы: n:=10.
Вектор случайных чисел: N:=runif(m, a, b)/
Построение гистограммы:
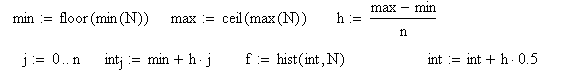
Рис. 3.9. Гистограмма равномерного закона распределения
- биномиальное распределение было получено Бернулли и является дискретным распределением, при котором случайное событие может иметь два и только два исхода: благоприятный (например, достигнут успех, получено годное изделие) и неблагоприятный (работа не выполнена, изделие с браком) (рис. 3.10). Вероятность k удачных исходов в n реализациях некоторого эксперимента равна
, (3.14)
где p – вероятность успеха в каждом испытании. В системе MathCAD имеется функция биномиального распределения rbinom(m,n,p);
- геометрическое распределение – это модель, которая описывает число испытаний n с вероятностью успеха p, необходимых для появления первого успешного результата (включая также и этот результат). Он является частным случаям биномиального распределения для k=1, поэтому
(3.15)
Это распределение применяется к статистике редко встречающихся событий (возникновение аварийных ситуаций, эпидемий, несчастных случаев и т.д.). В системе MathCAD имеется функция геометрического распределения rgeom(m,p) (рис. 3.10).
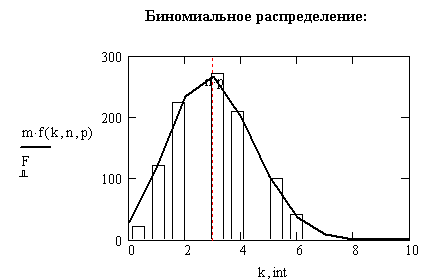
Рис.3.10. Гистограмма биномиального закона распределения
- распределение Пуассона является моделью для описания числа появления редких случайных событий, которые могут принимать только два значения (свободно – занято, годное изделие – брак и т.д.) (рис. 3.11). Это распределение возникает в тех случаях, когда наступление некоторого признака имеет малую вероятность p, а число испытаний n достаточно большое. Вероятность f(k) того, что в n независимых испытаний событие наступит k раз, равна
. (3.16)
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру распределения a=n∙p. Дополнительным признаком распределения Пуассона является высокая вероятность появления нулевого числа событий в любом интервале времени. Формула Пуассона дает вероятность появления каких-то однородных событий, следующих друг за другом в какие-то моменты времени, то есть образующих поток событий. В системе MathCAD имеется функция распределения Пуассона rpois(m,λ).
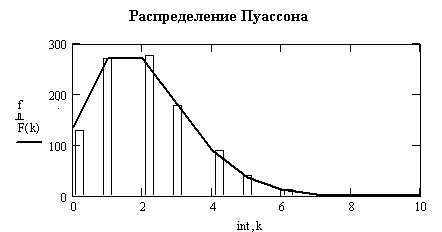
Рис. 3.11. Гистограмма распределения Пуассона
- нормальное распределение вероятностей занимает особое место среди различных теоретических законов, так как им описываются большинство случайных явлений, связанных с измерениями (рис. 3.12). К случайным явлениям, подчиняющимся нормальному закону распределения, относятся ошибки измерений производственных параметров, распределение технологических погрешностей, рост и вес большинства биологических объектов и т.д. Уравнение, описывающее плотность вероятности нормального распределения, имеет вид:
(3.17)
Таким образом, нормальное распределение характеризуется двумя параметрами: μ и σ и на графике представляет собой симметричную кривую Гаусса, имеющую максимум в точке х = μ. Точка перегиба кривой находится на расстоянии σ от центра распределения. Между абсциссами μ — σ и μ + σ расположено 68,3% всей площади кривой нормального распределения. Площадь, заключенная между ординатами, проведенными на расстоянии 2σ с той и другой стороны от центра, составляет 95,4% и, наконец, 99,7% площади находится в пределах μ ± 3σ.
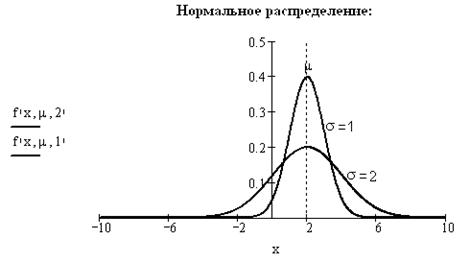
Рис. 3.12. График нормального распределения
Нормальное распределение является основным во многих практических исследованиях. Условия его возникновения связаны с центральной предельной теоремой, впервые сформулированной П.Л. Чебышевым. Она утверждает, что распределение какого-либо признака (параметра) при действии на него большого числа независимых причин сводится к нормальному, независимо от вида исходного распределения. Условия изготовления многих деталей и компонентов большинства промышленных изделий характеризуются именно воздействием на них большого числа независимых факторов: различных свойств материалов, квалификации операторов процесса, колебаний параметров окружающей среды, напряжения питания и т.д. Однако нормальное распределение не является единственно возможным. В системе MathCAD имеется функция нормального распределения rnorm();
- логарифмически нормальное распределение (кратко его называют логнормальным) – это такая статистическая модель, в которой нормальное распределение имеет логарифм случайной величины:
. (3.18)
Логарифмическое преобразование случайных величин используется для лучшего приближения ассиметричных распределений к нормальным законом, которые характерны для явлений, записываемых только положительными случайными числами. Например, время износа оборудования, срок службы различных компонентов, образование индекса цен, распределение доходов и т.д. По логарифмически нормальному закону распределены закономерности отказов радиоэлектронной аппаратуры в период ее старения. В системе MathCAD имеется функция логнормального распределения rlnorm() (рис. 3.13).
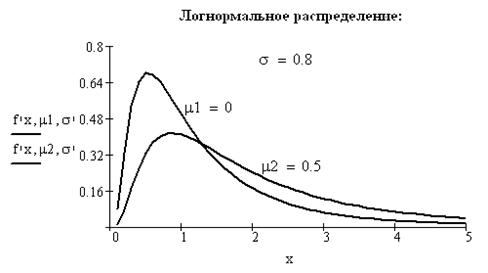
Рис.3.13. График логнормального распределения
- экспоненциальное распределение или показательное распределение описывается законом:
, (3.19)
где λ > 0 – параметр этого распределения. Экспоненциальное распределение является непрерывным аналогом дискретного геометрического распределения. Считается, что по показательному закону распределены, например, длительности выполнения отдельных операций в технологических процессах, интервалы времени между последовательными отказами в электронной аппаратуре и других сложных механизмах. Экспоненциальное распределение является основным в теории марковских процессов, так как оно обладает свойством отсутствия последействия, то есть последовательные моменты наступле
ния каких-то событий (телефонных вызовов, отказов аппаратуры, прибытия клиентов и т.д.) распределены на оси времени независимо друг от друга. В системе MathCAD имеется функция экспоненциального распределения rexp() (рис. 3.14).
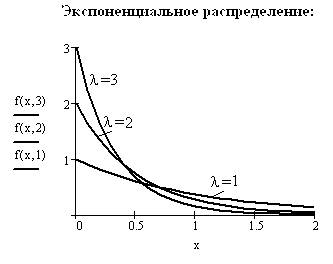
Рис.3.14. Экспоненциальное распределение
- распределение Вейбулла было специально разработано для использования в теории надежности и описания времени безотказной работы сложной радиоэлектронной аппаратуры. Функция плотности вероятности распределения Вейбулла описывается законом:
, (3.20)
где β – параметр формы, λ – параметр масштаба. В зависимости от значения параметра β распределение Вейбулла либо совпадает с экспоненциальным (при β=1), либо приближается к логарифмически нормальному (при β>1) (рис. 3.15).
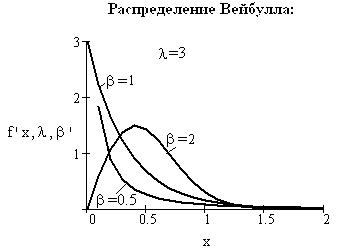
Рис. 3.15. Распределение Вейбулла
Наряду с экспоненциальным распределение Вейбулла широко применяется при оценках надежности. Одна из главных причин – наличие второго параметра β. Подбирая λ и β, можно добиться более полного соответствия теоретического закона распределения опытным данным, чем экспоненциального, зависящего только от параметра λ. В системе MathCAD имеется функция распределения Вейбулла rweibull();
- распределение Стьюдента используется при выборочных методах контроля по данным из небольших партий изделий. Эти методы разработаны английским математиком Карлом Госсетом в 1908 г. Однако он работал в частной фирме и по условиям контракта не мог их открыто высказывать, поэтому вынужден публиковать свои работы под псевдонимом Стьюдент, т.е. студент. Под этим названием и известно его распределение (рис. 3.16).
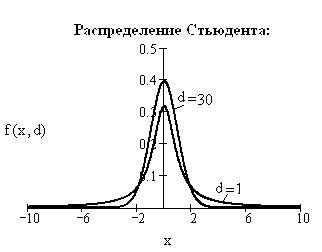
Рис. 3.16. Распределение Стьюдента
Распределение Стьюдента симметрично, но более сплющено, чем кривая нормального распределения, и поэтому вытянуто на концах. В системе MathCAD имеется функция распределения Стьюдента rt().
Модели теории массового обслуживания
С помощью математической теории массового обслуживания решается обширный круг задач, в которых рассматриваются системы или процессы обслуживания. Задачи обслуживания по своему содержанию бывают самыми разнообразными и возникают в различных сферах человеческой деятельности.
К числу важнейших количественных характеристик задач массового обслуживания относятся: входящий поток требований на обслуживание, интенсивность потока требований, длительность обслуживания требований.
Входящим потоком называется порядок, в соответствии с которым в систему поступают требования (заявки) на обслуживание. В теории массового обслуживания рассматривается несколько разновидностей входящих потоков. Наибольший практический интерес представляет простейший входящий поток, при котором требования на обслуживание поступают случайно. Случайный характер поступления требований вызывает необходимость при решении задач массового обслуживания привлекать аппарат математической статистики и теории вероятности.
Интенсивность потока характеризуется средним числом требований, поступающих в систему обслуживания за единицу времени. Этот показатель определяется обычно на основе научного анализа, а также наблюдений и статистической обработки их результатов.
Длительность обслуживания – это время, необходимое на обслуживание одного требования. Оно может быть постоянной и случайной величиной. В большинстве случаев длительность обслуживания различных требований является случайной величиной и называется случайным временем обслуживания. Она зависит от множества факторов.
Пример 5. Пусть бригада рабочих выполняет ремонт оборудования (то есть устраняет его неисправности) на основе поступающих требований (заявок) на обслуживание. Примем следующие обозначения:
n – число требований (заявок) в очереди;
pn – вероятность образования очереди из n требований;
l — среднее число поступающих на обслуживание требований;
m — среднее число требований, которое может быть обслужено системой (пропускная способность системы);
nc — средняя длина очереди, то есть число требований в ней.
Вероятность образования очереди из требований равна
pn = (l/m)n(1 — l/m) (3.21)
Отношение l/m=k принято называть интенсивностью нагрузки, оно обозначает средний объем обслуживания в единицу времени.
Вероятность любого события должна отвечать условию
0 < p < 1. (3.22)
Средняя длина очереди требований определим по формуле
nc = (l/m)/(1 — l/m). (3.23)
В формулах (3.21) и (3.23) предусматривается условие, при котором
l/m < 1. (3.24)
Из приведенных формул следует, что регулирование очереди требований на обслуживание достигается за счет изменения значения интенсивности нагрузки. В свою очередь интенсивность нагрузки зависит от среднего числа поступающих требований l и пропускной способности обслуживающей системы m.
Таким образом, ставится задача выбрать такое значение m, при котором было бы обеспечено оптимальное соотношение между издержками, связанными с содержанием обслуживающей системы, и издержками из-за простоя оборудования, вызванного ожиданием обслуживания.
Расчет суммы издержек на содержание обслуживающей системы при различных ее вариантах сложности не представляет. Для определения издержек, вызванных простоем оборудования, необходимо знать:
tож – среднее время ожидания обслуживания;
tобс – среднее время непосредственного обслуживания.
Их сумма представляет собой среднее время, затрачиваемое на ожидание и обслуживание. Она зависит от длины средней очереди nc и среднего числа поступивших на обслуживание требований l:
tож + tобс = nc / l. (3.25)
Так как величина показателя l является обратной по отношению к средней длительности одного обслуживания, то среднее время непосредственного обслуживания
tобс = 1/ m.. (3.26)
Подставив в (3.25) из (3.23) и (3.26) получим
tож = 1/(m — l) + 1/ m. (3.27)
Выполним моделирование зависимости (3.21) как функции pn от k = λ/μ (рис. 3.17). При n = 1 имеем кривую p(k,1), определяющую среднюю длину очереди (3.23). При увеличении числа требований (заявок) в очереди (n) экстремум p(k,n) сме
щается вправо, а вероятность образования очереди уменьшается в зависимости от пропускной способности системы.
На рис. 3.18 представлена модель уравнений (3.25 – 3.27), в которых исключено tобс и tож. Она использована для получения диаграммы издержек, вызванных простоем оборудования (рис. 3.19).
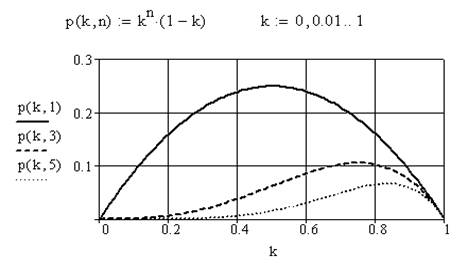
Рис. 3.17. Вероятность образования очереди pn в функции от λ/μ
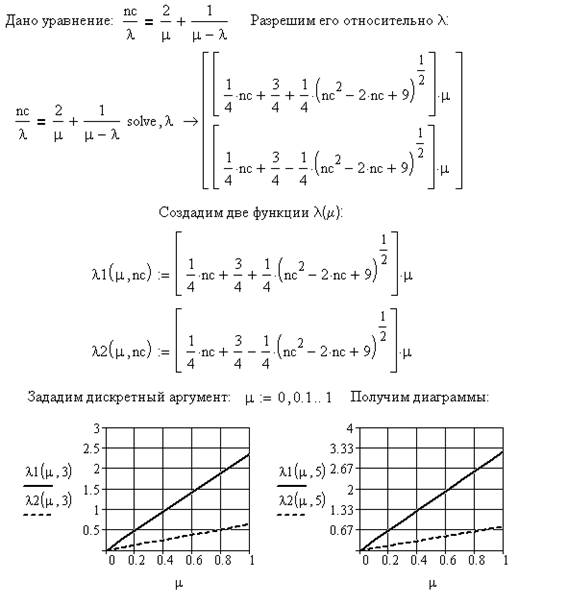
Рис. 3.18. Моделирование функции ?(?)
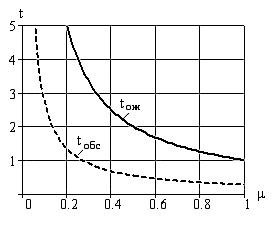
Рис.3.19. Среднее время ожидания и обслуживания клиента