Как было отмечено ранее, планом эксперимента называется совокупность опытов, необходимых для решения поставленной (в данном случае интерполяционной) задачи.
План эксперимента, необходимый для решения интерполяционной задачи, выбирают исходя из вида модели. Для линейной модели может быть применен наиболее простой план эксперимента – симметричный двухуровневый. Симметричный двухуровневый план предусматривает проведение опытов на двух уровнях, симметричных относительно некоторого уровня, выбранного в качестве исходного.
План эксперимента для двух- и трехфакторных функций отклика может быть изображен в виде графика. По осям графика откладываются значения факторов. Такой график называют факторным пространством.
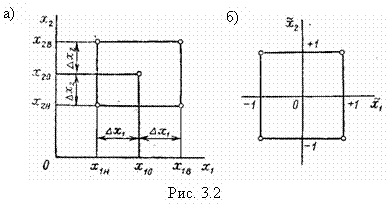
В качестве примера изобразим в факторном пространстве симметричный двухуровневый план для двухфакторной функции отклика (рис. 3.2, а):
y = f (x1, х2).
Здесь х1 0, х2 0 – исходные уровни факторов; х1 в, х2 в – верхние уровни; х1 н, х2 н – нижние уровни; Δx1, Δх2 – интервалы варьирования.
Верхний и нижний уровни факторов получают путем прибавления и вычитания из исходного уровня интервала варьирования:
![]()
Согласно плану эксперимента (рис. 3.2) опыты должны быть проведены на следующих уровнях факторов:
х1 в – х2 в; х1 н – х2 в; х1 в – х2 н; х1 н – х2 н (четыре опыта).
План эксперимента может быть также записан в виде таблицы, называемой матрицей планирования или репликой. Значения факторов записывают в реплику не в натуральном, а в нормированном (безразмерном) виде. Графически переход от натуральных значений факторов к нормированным означает перенос осей координат факторного пространства в исходный уровень (рис. 3.2, б). Нормированные значения факторов будем обозначать ![]() . Нормированные и натуральные значения факторов связаны между собой соотношениями:
. Нормированные и натуральные значения факторов связаны между собой соотношениями:
![]() (3.1)
(3.1)
где ![]() – исходный уровень и интервал варьирования j-го фактора; j – номер фактора.
– исходный уровень и интервал варьирования j-го фактора; j – номер фактора.
 |
Получим значения верхнего и нижнего уровней фактора в нормированном виде:
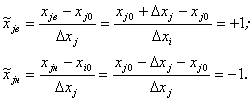
Таким образом, в нормированном виде верхний уровень любого фактора всегда равен 1, а нижний равен -1.
Исходный уровень любого фактора в нормированном виде всегда равен нулю:
![]()
Интервал варьирования любого фактора в нормированном виде всегда равен единице:
![]()
В качестве примера запишем матрицу планирования (реплику) симметричного двухуровневого плана для двухфакторной функции отклика (табл. 3.1), содержащую 4 опыта.
Реплики больших размерностей записывают следующим образом. Реплика для трехфакторной функции отклика y = f (x1, х2, х3) содержит 8 опытов (вершины куба в трехмерном факторном пространстве). Сначала записывают реплику двухфакторной функции отклика при значении фактора ![]() , затем при
, затем при ![]() (табл. 3.2).
(табл. 3.2).
Аналогично поступают с матрицами больших размерностей. Для четырехфакторной функции отклика записывают реплику трехфакторной функции отклика при ![]() , затем при
, затем при ![]() и т.д.
и т.д.
Таким образом, построение плана эксперимента заключается в написании соответствующей реплики. Для последующего осуществления эксперимента необходимо от нормированных значений факторов в реплике перейти к натуральным значениям по известной формуле:
![]() .
.
Для этого нужно знать исходный уровень каждого фактора (![]() ) и интервал варьирования (
) и интервал варьирования (![]() ). При решении интерполяционной задачи выбор исходных уровней и интервалов варьирования факторов осуществляется из следующих соображений. Полученное уравнение регрессии (модель) будет справедливо лишь для области, ограниченной верхними и нижними уровнями факторов, экстраполяция уравнения регрессии за их пределы неправомерна. Поэтому, определив область варьирования факторов с помощью системы ограничивающих зависимостей, выбирают исходный уровень возможно ближе к центру области варьирования, а верхний и нижний уровни – ближе к границам.
). При решении интерполяционной задачи выбор исходных уровней и интервалов варьирования факторов осуществляется из следующих соображений. Полученное уравнение регрессии (модель) будет справедливо лишь для области, ограниченной верхними и нижними уровнями факторов, экстраполяция уравнения регрессии за их пределы неправомерна. Поэтому, определив область варьирования факторов с помощью системы ограничивающих зависимостей, выбирают исходный уровень возможно ближе к центру области варьирования, а верхний и нижний уровни – ближе к границам.
Таблица 3.1
|
Номер опыта |
|
|
|
1 2 3 4 |
+1 -1 +1 -1 |
+1 +1 -1 -1 |
Таблица 3.2
|
Номер опыта |
|
|
|
|
1 2 3 4 5 6 7 8 |
+1 -1 +1 -1 +1 -1 +1 -1 |
+1 +1 -1 -1 +1 +1 -1 -1 |
+1 +1 +1 +1 -1 -1 -1 -1 |