Функция  называется выпуклой на выпуклом множестве , если для любых точек  и произвольного числа  выполняется неравенство:

.                   (3.12)

Функция  называется вогнутой на выпуклом множестве , если для любых точек  и произвольного числа  выполняется неравенство:

.                   (3.13)

Иногда выпуклую функцию называют выпуклой вниз в отличие от вогнутой функции, которую иногда называют выпуклой вверх. Смысл этих названий ясен из геометрического изображения типичной выпуклой (рис. 3.3) и вогнутой (рис. 3.4) функции.

Рис. 3.3. Выпуклая функция

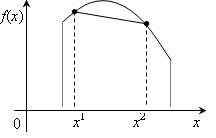
Рис. 3.4. Вогнутая функция

Подчеркнем, что определения выпуклой и вогнутой функций имеют смысл только для выпуклого множества X, так как только в этом случае точка  обязательно принадлежит Х.

Задачей выпуклого программирования называется частный случай общей задачи математического программирования (3.7), (3.8), когда целевая функция  и функции ограничений  являются вогнутыми на выпуклом множестве R.

Так как задача максимизации функции эквивалентна задаче минимизации этой функции со знаком «минус», ограничение  эквивалентно неравенству   и из вогнутости  следует выпуклость   и наоборот. Отсюда

задачей выпуклого программирования называется также задача минимизации выпуклой функции  при ограничениях:

, ,

где  – выпуклые функции; R – выпуклое множество. Это просто другая форма задачи.

Следует обратить внимание, что если задача выпуклого программирования формулируется как задача на максимум, то целевая функция обязательно вогнута, а если формулируется как задача на минимум – то выпукла, Если ограничения записываются в виде , то функции ограничений вогнуты, если ограничения записываются в виде , то функции ограничений выпуклы. Эта связь обусловлена наличием определенных свойств у задачи выпуклого программирования, которые при нарушении такой связи могут отсутствовать. Два основных таких свойства сформулированы в следующей лемме.

Лемма 1

Множество допустимых планов задачи выпуклого программирования

                                     (3.14)

является выпуклым. Любой локальный максимум вогнутой функции  на Х является глобальным.

Если бы функции ограничений  были выпуклы, то для определяемого множества Х (3.14) выпуклость уже бы не следовала. В этом случае можно доказать выпуклость множества:

.

Если бы целевая функция  была выпукла, то утверждение леммы относительно ее максимумов стало бы неверным, однако аналогичное утверждение можно было бы доказать для минимумов.

Функция  называется строго выпуклой на выпуклом множестве , если для любых точек , и произвольного числа  выполняется неравенство .

Функция  называется строго вогнутой на выпуклом множестве , если для любых точек , и произвольного числа  выполняется неравенство:

.

Лемма 2

Сумма выпуклых (вогнутых) функций выпукла (вогнута). Произведение выпуклой (вогнутой) функции на положительное число выпукло (вогнуто). Сумма выпуклой (вогнутой) и строго выпуклой (строго вогнутой) функций строго выпукла (строго вогнута).

Теорема 1

Если функция  строго вогнута (строго выпукла) на выпуклом множестве Х, то у нее может быть только одна точка максимума (минимума).

Доказательство

Предположим противное, т.е. что существует две точки , , являющиеся точками максимума строго вогнутой функции  на Х. Обозначив , имеем . Тогда для любого   справедливо: 

и

,

т.е. пришли к противоречию. Аналогично доказывается для минимума строго выпуклой функции.

Линейная функция  представляет собой единственный пример одновременно выпуклой и вогнутой функции, значит, она не является строго выпуклой (строго вогнутой). Квадратичная функция  может быть не выпуклой (вогнутой), а может быть строго выпуклой (строго вогнутой); все это определяется матрицей D. Элементы матрицы D представляют собой вторые частные производные квадратичной функции, т.е.

.

Обозначим матрицу вторых частных производных через .

Лемма 3

Для того чтобы квадратичная функция  была выпуклой (вогнутой) на всем пространстве , необходимо и достаточно, чтобы матрица D была положительно (отрицательно) определена. Если D положительно (отрицательно) определена, т.е.

 (),

то  строго выпукла (строго вогнута).

Задача максимизации (минимизации) квадратичной функции при линейных ограничениях, где D – отрицательно (положительно) определенная матрица, причем D^T=D, называется задачей квадратичного программирования.

Из леммы вытекает, что рассмотренная в разделе 2 задача линейного программирования, как и задача квадратичного программирования, представляет собой частный случай задачи выпуклого программирования.

Бывают функции, которые выпуклы по одной группе переменных и вогнуты по другой. Такие функции представляют собой один из основных классов функций, у которых заведомо существует седловая точка.

Теорема 2

(О существовании седловой точки у вогнуто-выпуклой функции). Пусть X и Y суть выпуклые замкнутые ограниченные подмножества конечномерных евклидовых пространств, а функция  – непрерывна по  и , вогнута по  и выпукла по , тогда имеет на  седловую точку.

Рассмотрим функцию Лагранжа для задачи выпуклого программирования:

             (3.15)

определенную на прямом произведении , где . Эта функция в силу вогнутости ,  является вогнутой по  и линейной, а следовательно, выпуклой по .

Однако нельзя утверждать на основании теоремы 1, что она имеет седловую точку, так как множество R не обязательно является замкнутым и ограниченным, а Y заведомо неограниченно. Тем не менее, можно ожидать, что при некоторых условиях седловая точка все же будет существовать.

Наиболее известной теоремой, относящейся к этому вопросу, является теорема Куна-Таккера, которая устанавливает связь между существованием решения задачи выпуклого программирования и седловой точки у функции Лагранжа при выполнении условия Слейтера: задача выпуклого программирования удовлетворяет условию Слейтера, если существует такая точка , что выполняется условие: .

Теорема Куна-Таккера

Если задача выпуклого программирования удовлетворяет условию Слейтера, то необходимым и достаточным условием оптимальности плана  является существование такого , что пара  является седловой точкой функции Лагранжа (3.15) на .

То, что условие Слейтера является существенным, показывает следующий пример.

Пример 1

Дана задача выпуклого программирования:

.

Здесь, очевидно, что x = 0 есть решение задачи, но у функции Лагранжа  седловой точки нет, так как внешняя грань в минимаксной задаче не достигается:

.

Разбиение ограничений в задаче выпуклого программирования на  и , как уже говорилось, является условным. Поэтому обычно под R понимается множество простого вида, это либо все пространство E_n, либо неотрицательный ортант, либо параллелепипед. Сложность же задачи выпуклого программирования определяется системой ограничений:

.

Так как седловая точка функции Лагранжа ищется на произведении множеств , где Y также является множеством простого вида (неотрицательным ортантом), то смысл теоремы Куна-Таккера состоит в сведении задачи поиска экстремума функции со сложными ограничениями на переменные к задаче поиска экстремума новой функции с простыми ограничениями.

Если множество R совпадает с E_n, то условия экстремума, как известно, имеют вид:

.           (3.16)

Причем эти условия являются не только необходимыми, для того чтобы функция  достигала в точке  максимума по , но и достаточными. Это – важное свойство вогнутых функций, а  для задачи выпуклого программирования вогнута по .

Теорема 3

Для того чтобы непрерывно дифференцируемая вогнутая функция  имела в точке  максимум на E_n, необходимо и достаточно, чтобы градиент функции  в точке  был равен нулю, т.е. .

Вспомним, что градиент функции равен:

.

Таким образом, для нахождения седловой точки функции Лагранжа  на произведении , а следовательно, и для нахождения решения  задачи выпуклого программирования при R=E_n надо решить систему уравнений (3.16). Но в этой системе n уравнений, а неизвестных n+m, так как помимо n-мерного вектора  нам неизвестен и m-мерный вектор множителей Лагранжа . Однако для седловой точки функции Лагранжа выполняется очень важное свойство:

.                    (3.17)

Из уравнения (3.17) вытекает, что либо , либо , либо то и другое одновременно. Это свойство аналогично второй теореме двойственности (подразд. 2.5) линейного программирования. Ограничения, которые выполняются в некоторой точке как равенства, называются активными.

Таким образом, только те множители Лагранжа  могут быть отличны от нуля, которые соответствуют активным в точке  ограничениям. С учетом этого свойства для нахождения решения задачи выпуклого программирования рассмотрим следующий способ.

Введем множество:

.

Это множество представляет собой совокупность индексов активных в точке  ограничений. Тогда можно утверждать в силу сказанного выше, что . Поэтому для определения  и ненулевых  имеем систему уравнений:

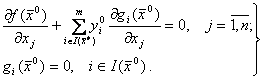                 (3.18)

Число неизвестных и число уравнений в этой системе совпадают, поэтому, в принципе, находя решение системы (3.18), тем самым решим исходную задачу выпуклого программирования. Система (3.18) представляет собой необходимые и

достаточные условия оптимальности для задачи выпуклого программирования в случае, когда R = E_n.

Если R является неотрицательным ортантом, т.е.

,

то для каждой компоненты  решения задачи выпуклого программирования возможны две альтернативы: либо , либо . Для первой альтернативы условия оптимальности совпадают со случаем R=E_n, т.е. имеют вид (3.16) (при данном j). Для второй альтернативы это не так.

Если  является компонентой точки максимума функции  по  в области , то можно утверждать, что необходимо (а для вогнутой функции и достаточно) только выполнения неравенства

,              (3.19)

т.е. функция  должна не возрастать по  при движении внутрь области .

Но так как , то можно записать:

.                 (3.20)

Объединяя обе альтернативы, т.е. учитывая выражения (3.16), (3.19), (3.20) для задачи выпуклого программирования в случае,  можно представить в виде

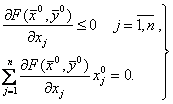                (3.21)

Так как , то из условий (3.21) следует, что либо , либо . Таким образом, как и в случае R=E_n, имеем n уравнений, которые вместе с уравнениями для активных ограничений определяют  и .

Пример 2

Найти  при ограничении .

Здесь . Функция  линейная и поэтому максимум достигается на границе допустимого множества. Используя условия (3.18), имеем систему трех уравнений с тремя неизвестными:

,

откуда

(другое решение дает минимум).

В общем случае, когда R – произвольное выпуклое множество, необходимые и достаточные условия оптимальности для задачи выпуклого программирования формулируются с помощью производных по направлению.