Одним из важнейших следствий уравнений Максвелла является существование электромагнитных волн. Для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей  и  переменного электромагнитного поля удовлетворяют волновому уравнению типа (3.14):

,                                              (3.17)

,                                             (3.18)

где 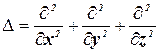 – оператор Лапласа, v – фазовая скорость волны.

Фазовая скорость электромагнитных волн определяется выражением:

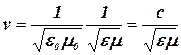,                                      (3.19)

где ,  и  – соответственно электрическая и магнитная постоянные,  и  – соответственно электрическая и магнитная проницаемости среды.

Следствием теории Максвелла является поперечность электромагнитных волн: векторы  и взаимно перпендикулярны и колеблются в одинаковой фазе. Соотношение между ними дается выражением

.                                            (3.20)

От уравнений (3.17) и (3.18), в случае плоской волны, можно перейти к уравнениям:

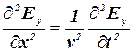,                                                  (3.21)

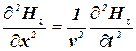,                                                 (3.22)

где соответственно индексы y и z при  и  подчеркивают лишь то, что векторы  и  направлены вдоль взаимно перпендикулярных осей y и z.

Решением уравнений (3.21) и (3.22) являются уравнения:

,                                        (3.23)

,                                       (3.24)

где Е₀ и Н₀ – соответственно амплитуды напряженностей электрического и магнитного полей волны; w – круговая частота волны;  – волновое число; j – начальная фаза колебаний в точках с координатой х = 0. В уравнениях (3.23) и (3.24) j одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковых фазах.