Определение. Функция j (x), определенная на множестве X дуг транспортной сети D, и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если:
а) для любой дуги x 
X величина j(x), называемая потоком по дуге х, удовлетворяет условию 0 
j(x) c(x);
б) для любой промежуточной вершины v выполняется равенство
т.е. сумма потоков по дугам, заходящими в v, равна сумме потоков по дугам, исходящими из v.
Определение. Величиной потока j в транспортной сети D называется величина j, равная сумме потоков по всем дугам, заходящим в vn, или, что то же самое, величина, равная сумме потоков по всем дугам, исходящим из v1, т.е.
Пусть j — допустимый поток в транспортной сети D.
Определение. Дуга x 
X называется насыщенной, если поток по ней равен ее пропускной способности, т.е. если j(x) = c(x). Поток j называется полным, если любой путь в D из v1 в vn содержит, по крайней мере, одну насыщенную дугу.
Определение. Поток j называется максимальным, если его величина принимает максимальное значение по сравнению с другими допустимыми потоками в транспортной сети D.
Очевидно, что максимальный поток j обязательно является полным. Обратное неверно. Существуют полные потоки, не являющиеся максимальными. Тем не менее, полный поток можно рассматривать как некоторое приближение к максимальному потоку.
Алгоритм построения полного потока в транспортной сети D:
Шаг 1. Полагаем "x 
X j(x) = 0 (т.е. начинаем с нулевого потока). Кроме того, полагаем D` = D.
Шаг 2. Удаляем из орграфа D` все дуги, являющиеся насыщенными при потоке j в транспортной сети D. Полученный орграф снова обозначаем через D`.
Шаг 3. Ищем в D` простую цепь h из v1 в vn. Если такой цепи нет, то j — искомый полный поток в транспортной сети D. В противном случае переходим к шагу 4.
Шаг 4. Увеличиваем поток j(x) по каждой дуге x из h на одинаковую величину a > 0 такую, что, по крайней мере, одна дуга из h оказывается насыщенной, а потоки по остальным дугам из h не превышают их пропускных способностей. При этом величина потока также увеличивается на a, а сам поток j в транспортной сети D остается допустимым (поскольку в каждую промежуточную вершину, содержащуюся в h, дополнительно вошло a единиц потока и из нее вышло также a единиц потока). После этого переходим к шагу 2.
Пример 90.
Построить полный поток в транспортной сети, изображенной на рис. 3.24.
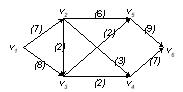
Рис. 3.24. Транспортная сеть из примера 90
Решение.
Начинаем с нулевого потока (рис. 3.25). Пошагово выделяем простые цепи и увеличиваем поток по ним таким образом, чтобы хотя бы одна дуга в каждой из них стала насыщенной. Полученную насыщенную дугу помечаем пунктиром, помня, что по насыщенной дуге больше идти нельзя.
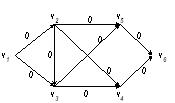
Рис. 3.25. Построение полного потока (шаг 1)
1) h 1 = v1v2v4v6, a1 = min{7, 3, 7} = 3 (рис. 3.26).
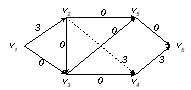
Рис. 3.26. Построение полного потока (шаг 2)
2) h 2 = v1v2v3v4v6, a2 = min{7-3, 2, 2, 7-3} = 2 (рис. 3.27).
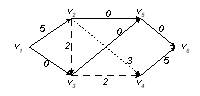
Рис. 3.27. Построение полного потока (шаг 3)
3) h 3 = v1v3v5v6, a3 = min{8, 2, 9} = 2 (рис. 3.28).
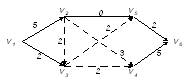
Рис. 3.28. Построение полного потока (шаг 4)
4) h 4 = v1v2v5v6, a4 = min{7-5, 6, 9-2} = 2 (рис. 3.29).
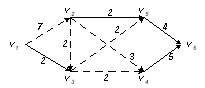
Рис. 3.29. Построение полного потока (шаг 5)
Заметим, что в полученной транспортной сети не существует пути из источника в сток, по которому возможно пройти. Следовательно, построенный поток в транспортной сети является полным и j = 3+2+2+2=9.