Выделим для заданной транспортной сети D и допустимого потока j в этой сети орграф приращений I(D, j), имеющий те же вершины, что и сеть D. Каждой дуге x = (v, w)X транспортной сети D в орграфе приращений I(D, j) соответствуют две дуги: x и x` = (w,v) — дуга, противоположная по направлению дуге x. Припишем дугам x = (v, w)ÎX, x` = (w, v) орграфа приращений I(D, j) длину l:

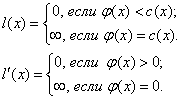
т.е. орграф I(D, j) является нагруженным. При этом, очевидно, что длина любого пути из v₁ в v_n в орграфе I(D, j) равна либо 0, либо .

Пример 91.

Построить орграф приращений для данной транспортной сети и построенного полного потока в этой сети.

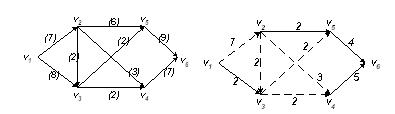
Рис. 3.30. Транспортная сеть для примера 91

Решение.

Напомним, что орграф приращений имеет в два раза больше дуг, чем исходная транспортная сеть.

Для дуги прямой направленность вес равен 0, если дуга не является насыщенной,  — в противном случае. Для дуги обратной направленности вес равен 0, если поток по ней не равен нулю,  — в противном случае. На рис. 3.31 изображен орграф приращений, соответствующий данному потоку в исходной транспортной сети.

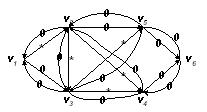
Рис. 3.31. Орграф приращений