Если передаточная функция замкнутой устойчивой дискретной системы описывается дробно-рациональным выражением
то степень устойчивости такой системы может быть оценена по расстоянию от единичной окружности, проведенной из начала координат плоскости z, до ближайшего к ней z-корня характеристического уравнения:
При использовании для описания дискретной САУ комплексной переменной р степень устойчивости оценивается по расстоянию от мнимой оси р-плоскости до ближайшего к ней р-корня характеристического уравнения:
Если первые k младших коэффициентов характеристического уравнения равны нулю, т.е. 
, оно сводится к виду:
Это уравнение имеет корень 
кратности k, при этом степень устойчивости оказывается бесконечно большой.
Определим решетчатую функцию на выходе такой абсолютно устойчивой дискретной системы при подаче на вход единичного ступенчатого сигнала. Для системы второго порядка Z-изображение выходного сигнала равно:
Значения решетчатой функции 
определим путем разложения 
в ряд Лорана:
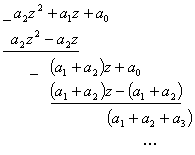
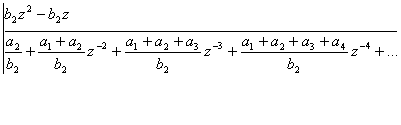
Имеем:
; 
;
при 
.
То есть выходной сигнал системы, достигнув установившегося значения за два периода квантования, в дальнейшем остается неизменным.
В общем случае для абсолютно устойчивой системы k-го порядка значения решетчатой переходной функции
при 
,
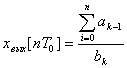а при 
,
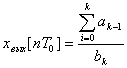то есть по истечении k тактов выходной сигнал системы становится постоянным.
Следовательно, переходный процесс, вызванный единичным ступенчатым воздействием, заканчивается за конечное время 
. Необходимо учитывать, что между моментами квантования непрерывный сигнал 
может содержать пульсации, но при малом периоде квантования 
их амплитуда обычно незначительна.
Пример 21
Необходимо определить значения коэффициентов 
и 
, при которых достигается конечная длительность процесса регулирования в дискретной САУ (рис. 3.2).
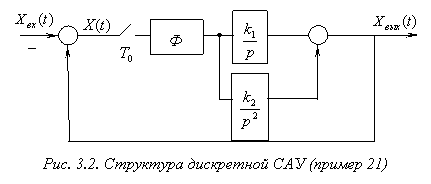Дискретная передаточная функция разомкнутой системы:
.
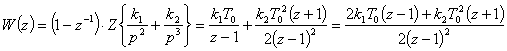Характеристическое уравнение замкнутой САУ:
или
Следовательно, условие конечной длительности переходного процесса имеет вид:
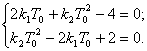
Решение приведенной системы уравнений:
; 
.
Время переходного процесса равно:
.