Рассмотрим особенности построения математических схем при дискретно-стохастическом подходе к формализации процесса функционирования исследуемой системы  S. Так как сущность дискретизации  времени  при  этом  подходе  остается   аналогичной рассмотренным в пункте 3.3 конечным автоматам, то влияние фактора стохастичности проследим также на разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.

Основные соотношения. В общем виде вероятностный автомат (англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.

Применение схем вероятностных автоматов (Р-схем) имеет важное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.

Введем математическое понятие Р-автомата, используя понятия для F-автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (x_i, z_s), где x_i и z_s — элементы входного подмножества X и подмножества состояний Z соответственно.

Определение 3.1. Если существуют две такие функции φ и ψ, что с их помощью осуществляются отображения  G→Z  и  G→Y,  то говорят, что F = <Z, X, Y, φ, ψ> определяет автомат детерминированного типа.

Введем в рассмотрение более общую математическую схему. Пусть Ф — множество всевозможных пар вида (z_k, у_j), где у_j — элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

При этом  , где b_kj — вероятности перехода автомата в состояние z_k и появления на выходе сигнала  y_i,  если он был в состоянии z_s, и на его вход в этот момент времени поступил сигнал x_i. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов P = <Z, X, Y, B> называется вероятностным автоматом (Р-автоматом).

Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, что можно представить соответственно в виде:

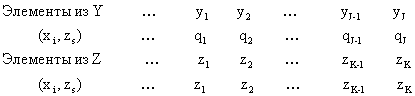
При этом   и  ,  где z_k и q_k — вероятности перехода Р-автомата в состояние z_k и появления выходного сигнала y_k при условии, что Р-автомат находился в состоянии z_s и на его вход поступил входной сигнал х_i.

Если для всех k и j имеет место соотношение q_kz_i = b_kj, то такой Р-автомат называется вероятностным автоматом Мили. Это требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.

Пусть теперь определение выходного сигнала Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы. Другими словами, пусть каждый элемент выходного подмножества У индуцирует распределение вероятностей выходов, имеющее следующий вид:

Здесь  ,  где s_i – вероятность появления выходного сигнала y_i при условии, что Р-автомат находился в состоянии z_k.

Возможные приложения. Если для всех  k  и  i  имеет место соотношение  z_ks_i = b_ki, то такой Р-автомат называется вероятностным автоматом Мура. Понятие Р-автоматов Мили и Мура введено по аналогии с детерминированным F-автоматом, задаваемым F = <Z, X, Y, φ, ψ>.  Частным случаем Р-автомата, задаваемого как P = <Z, X, У, B>, являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминированно. Если выходной сигнал Р-автомата определяется детерминированно, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z-детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.

Пример 3.4. Рассмотрим Y-детерминированный Р-автомат, который задан таблицей переходов (см. табл. 3.6) и таблицей выходов:

В этих таблицах  p_ij — вероятность перехода Р-автомата из состояния z_i в состояние z_j. При этом, как и ранее,.

Первую из этих таблиц можно представить в виде квадратной матрицы размерности К х К, которую будем называть матрицей переходных вероятностей или просто матрицей переходов Р-автомата. В общем случае такая матрица переходов имеет вид

Таблица 3.6

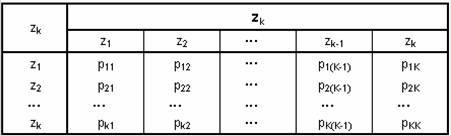
Для описания Y-детерминированного Р-автомата необходимо задать начальное распределение вероятностей вида

Здесь d_K — вероятность того, что в начале работы Р-автомат находится в состоянии k. При этом  .

Будем считать, что до начала работы (до нулевого такта времени) Р-автомат всегда находится в состоянии z₀ и в нулевой такт времени меняет состояние в соответствии с распределением D. Дальнейшая смена состояний Р-автомата определяется матрицей переходов Р_Р. Информацию о начальном состоянии Р-автомата удобно внести в матрицу Рр, увеличив ее размерность до (K+1) х (К+ 1). При этом первая строка такой матрицы, сопоставляемая состоянию z₀, будет иметь вид (0, d_l, d₂, …, d_k), а первый столбец будет нулевым.

Описанный Y-детерминированный Р-автомат можно задать в виде ориентированного графа, вершины которого сопоставляются состояниям автомата, а дуги — возможным переходам из одного состояния в другое. Дуги имеют веса, соответствующие вероятностям перехода р_ij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями.

Пример 3.4. Пусть задан Y-детерминированный Р-автомат

;          .

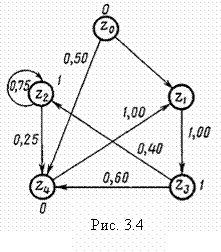На рис. 3.4 показан граф переходов этого вероятностного автомата. Требуется оценить суммарные финальные вероятности пребывания этого Р-автомата в состояниях z₂ и z₃.

При использовании аналитического подхода можно записать известные соотношения из теории марковских цепей и получить систему уравнений для определения финальных вероятностей. При этом начальное состояние z₀ можно не учитывать, так как начальное распределение не оказывает влияния на значения финальных вероятностей. Тогда имеем

; ,

где  с_k – финальная вероятность пребывания Р-автомата в состоянии z_k.

Получаем систему уравнений

Добавим к этим уравнениям условие нормировки  c₁ + с₂ + с₃ + с₄ = 1. Тогда, решая систему уравнений, получим с₁ = 5/23, с₂ = 8/23, с₃ = 5/23, с₄ = 5/23. Таким образом, с₂ + с₃ = 13/23 =0,5652. Другими словами, при бесконечной работе заданного в этом примере Y-детерминированного Р-автомата на его выходе формируется двоичная последовательность с вероятностью появления единицы, равной 0,5652.

Подобные Р-автоматы могут использоваться как генераторы марковских последовательностей, которые необходимы при построении и реализации процессов функционирования систем S или воздействий внешней среды Е.

Для оценки различных характеристик исследуемых систем, представляемых в виде Р-схем, кроме рассмотренного случая аналитических моделей можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.