Эксперимент, число опытов которого равно числу возможных сочетаний уровней плана, называется полным факторным экспериментом (ПФЭ).

Число возможных сочетаний уровней симметричного двухуровневого плана равно:

N = 2^K,

где К – число факто­ров.

В соответствии с этим ПФЭ, выполняемый по симмет­ричному двухуровневому плану, называется ПФЭ типа 2^K. Для двухфакторной функции отклика число опытов ПФЭ со­ставляет N =2 ^K = 2² = 4, для трехфакторной N = 2^К = 2³ = 8. Следовательно, матрицы планирования (см. табл. 3.1, 3.2), являются матрицами ПФЭ. Матрицы ПФЭ иначе называют полными репликами.

Матрица ПФЭ (полная реплика) обладает следующими свойствами:

1) алгебраическая сумма элементов столбца каждого фактора равна нулю:

где i – номер опыта; N – число опытов; j – номер фактора. Это свойство вытекает из симметричности плана относи­тельно начала координат и называется симметричностью;

2) сумма квадратов элементов столбца каждого фактора равна числу опытов6

.

Это свойство вытекает из того, что факторы представлены в матрице в нормированном виде, и называется условием нормировки;

3) сумма почленных произведений любых двух столбцов матрицы равна нулю:

.

Это свойство называется ортогональностью.

Таким образом, матрица ПФЭ типа 2^К симметрична, ортогональна и отвечает условию нормировки.

С помощью таких свойств полной реплики, как симметричность и условие нормировки, можно значительно упростить процесс вычисления коэф­фициентов модели. Запишем матрицу ПФЭ (полную реплику) для однофакторной функции отклика y = f(x) (табл. 3.3). Она включает N = 2^К = 2¹ опыта. Эта матрица симметрична и отвечает усло­вию нормировки. Допустим, что мы провели эксперимент согласно нашему плану (см. табл. 3.3) и получили экспе­риментальные значения функции отклика у:

у = y₁               при     = 1;

у = у₂                при    = -1.

Таблица 3.3

Коэффи­циенты в линейной модели  вычисляются, как было указано в подразделе 2.5  с помощью МНК по формулам (2.1) и (2.2).

Перейдем в уравнении регрессии к нормированному зна­чению фактора:

,

где  – исходный уровень и интервал варьирования фак­тора.

Объединим постоянные члены в уравнении регрессии путем введения коэффициентов:

 и .

Получаем уравнение регрессии в нормированном виде:

.

Коэффициенты и  могут быть также вы­числены с помощью формул МНК, (2.1) и (2.2).

Поскольку в силу симметричности и условия нормировки матрицы ПФЭ

;                 ,

получим:

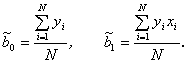
Легко показать, что для линейной модели двухфакторной зависимости  коэффициенты вычисля­ются по аналогичным формулам:

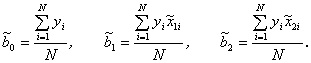
Отсюда вытекает общее правило: коэффициенты линейной модели многофакторной функции отклика у = f (х₁, х₂, …, х_k) вычисляются по следующим формулам:

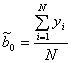;                                                          (3.2)

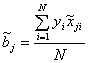                                                        (3.3)

где i – номер опыта; j – номер фактора.

Для того чтобы перейти к уравнению регрессии в натуральном виде, следует вместо нормированных значений факторов подставить их выражения через натуральные значения:

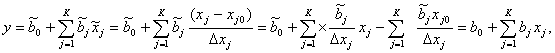
где 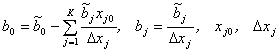 – исходные уровни и интервалы варьирования факторов, К – число факторов.