Основной задачей синтаксического анализа является выявление синтаксической структуры исходной программы. Как было показано ранее, одним из способов решения этой задачи является моделирование левого или правого вывода в грамматике, описывающей входной язык программирования, с помощью допускающего МП-автомата (МП-распознавателя). При этом МП-автомат моделирует, по существу, процесс построения дерева вывода. Однако собственно дерево вывода существует лишь во время функционирования МП-распознавателя в виде шагов его работы. Для получения «физического» представления дерева вывода в конструкцию и систему команд МП-распознавателя необходимо внести следующие изменения:
· снабдить его выходной лентой, на которую будет выполняться выдача информации о дереве вывода;
· определить дополнительные операции по построению дерева вывода на выходной ленте.
МП-распознаватель, снабженный выходной лентой, называют обычно МП-преобразователем. Для выдачи информации на выходную ленту МП-преобразователь использует специальную команду ВЫДАТЬ (X), где X — выводимая информация.
Структура МП-преобразователя показана на рис. 3.17.
В результате моделирования процесса синтаксического анализа правильной входной цепочки такой МП-преобразователь сформирует на выходной ленте линейное представление полученного дерева вывода.
Существуют различные способы линейного представления дерева вывода (основные из них будут рассмотрены), однако в любом случае для построения таких представлений требуется выполнить определенные действия (операции). Если эти операции ввести в систему команд МП-преобразователя, то это существенно усложнит разработку его управляющих таблиц и будут потеряны все преимущества определения МП-автомата как абстрактного устройства по переработке информации. Но есть и другая возможность, а именно, возложить на МП-преобразователь не выполнение действий (операций) по построению линейного представления дерева вывода, а лишь только получение такой последовательности действий (операций). И лишь после выполнения полученной последовательности действий с помощью другого устройства (интерпретатора), будет получено линейное представление дерева вывода-описание структуры программы (в данном контексте мы их будем отождествлять). При таком подходе нет необходимости вводить в систему команд МП-автомата команды, реализующие построение дерева. Достаточно лишь команды ВЫДАТЬ (X), где X — операционный символ, который для МП-преобразователя не имеет ни какого семантического смысла и является чисто синтаксической единицей. Другое преимущество такого определения — независимость описания работы МП-преобразователя от семантики операционных символов, трудоемкости выполнения этих операций, способа их реализации и т.д. Важен лишь их перечень и последовательность выполнения. Таким образом, в изложенной выше трактовке МП-преобразователь осуществляет перевод входной цепочки в выходную цепочку операционных символов, интерпретация (выполнение) которой обеспечит построение линейного представления дерева вывода. А так как перевод осуществляется с учетом синтаксиса входной цепочки, то такой перевод обычно называют синтаксически-управляемым переводом.
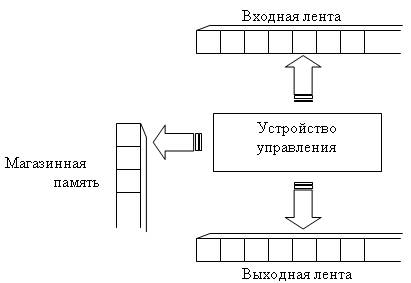
Рис. 3.17. Структура МП-преобразователя
Источником, по которому можно построить МП-преобразователь, является аппарат, получивший название синтаксически-управляемые схемы перевода. Воспроизведем основные формальные определения, применяемые при построении МП-преобразователя рассмотренного вида с использованием этого аппарата [4].
Определение 3.5.1. Пусть G = <N, T, P, S> — КС-грамматика и ![]() — множество операционных символов. Каждому правилу:
— множество операционных символов. Каждому правилу:
А0 ![]() x1A1x2…xnAnxn+1
x1A1x2…xnAnxn+1![]() P,
P,
где Ai![]() N, xi+1
N, xi+1![]() T*, 0
T*, 0![]() i
i![]() n будет соответствовать правило:
n будет соответствовать правило:
А0 ![]() y1A1y2…ynAnyn+1, yn+1
y1A1y2…ynAnyn+1, yn+1![]() .
.
Простой синтаксически-управляемой схемой (СУ-схемой) называется пятерка D = (T, ![]() , N, R, S), где R — множество пар правил:
, N, R, S), где R — множество пар правил:
(А0 ![]() x1A1x2…xnAnxn+1, А0
x1A1x2…xnAnxn+1, А0 ![]() y1A1y2…ynAnyn+1).
y1A1y2…ynAnyn+1).
Обозначим пару таких правил через (![]() ,
, ![]() ). Множество пар терминальных цепочек (x, y), синхронно выводимых из пары цепочек (S, S) с помощью СУ-правил (
). Множество пар терминальных цепочек (x, y), синхронно выводимых из пары цепочек (S, S) с помощью СУ-правил (![]() ,
,![]() ), называется простым управляемым переводом
), называется простым управляемым переводом ![]() (D) = {(x, y) | (S, S)*
(D) = {(x, y) | (S, S)* ![]() (x, y), x
(x, y), x![]() T*,
T*, ![]() }. СУ-правила будем записывать в виде
}. СУ-правила будем записывать в виде ![]() (подразумевая пару правил (
(подразумевая пару правил (![]() )).
)).
Процесс синтаксического анализа также можно представить в виде СУ-перевода, в котором выходная цепочка — это последовательность номеров подстановок, используемых при левом выводе входной цепочки (нисходящий анализ), или обращенной последовательности номеров подстановок, используемых при правом выводе (для восходящего анализа).
Пусть G = <N, Т, Р, S> — исходная КС грамматика, в которой все подстановки из множества правил Р пронумерованы числами 1, 2, …, р. Схема СУ-перевода для синтаксического анализа определяется как четверка [4]:
D = <N, {T![]() {1, 2, …, p}}, R, S>,
{1, 2, …, p}}, R, S>,
где схема подстановок R включает правила вида ![]() такие, что если
такие, что если ![]() — подстановкой из множества P с номером i, то
— подстановкой из множества P с номером i, то ![]() , где
, где ![]() — цепочка
— цепочка![]() из которой устранены все терминальные символы.
из которой устранены все терминальные символы.
Пример 3.5.1. Схема СУ-перевода для грамматики простых арифметических выражений определяется следующим образом:
D = <{E, T, F}, {+, *, (, ), i}![]() {1, 2, …, 6}}, R, S = {E}>,
{1, 2, …, 6}}, R, S = {E}>,
где множество R состоит из подстановок:
1) E![]() E+T, 1ET
E+T, 1ET
2) E![]() T, 2T
T, 2T
3) T![]() T*F, 3TF
T*F, 3TF
4) T![]() F, 4F
F, 4F
5) F![]() (E), 5E
(E), 5E
6) F![]() i, 6.
i, 6.
На рис. 3.18 изображена пара деревьев вывода, задающая перевод цепочки i*(i+i) в выходную цепочку, отвечающую левому выводу ее в исходной грамматике.
Функциональным интерпретатором схемы СУ-перевода является МП-преобразователь. Дадим формальное определение допускающего МП-преобразователя.
Определение 3.5.2. Недетерминированным МП-преобразователем называется восьмерка:
M = <Q, A, ![]() , Г,
, Г, ![]() , q0, z0, F>,
, q0, z0, F>,
где Q — множество состояний;
A,![]() , Г — входной, выходной и магазинный алфавиты соответственно;
, Г — входной, выходной и магазинный алфавиты соответственно;
q0![]() Q — начальное состояние;
Q — начальное состояние;
z0![]() Г — начальный символ магазинной памяти;
Г — начальный символ магазинной памяти;
F![]() Q — множество заключительных состояний;
Q — множество заключительных состояний;
![]() — отображения вида
— отображения вида ![]() : Qx{A
: Qx{A![]() {
{![]() }}xГ
}}xГ![]() QxГ*x
QxГ*x![]() *. Если отображение
*. Если отображение ![]() задается в виде совокупности команд МП-преобразователя, то команды будем записывать в виде:
задается в виде совокупности команд МП-преобразователя, то команды будем записывать в виде:
![]() (q, x, y) = (q’, z*, W*).
(q, x, y) = (q’, z*, W*).
Интерпретируется команда обычным путем (также как и для МП-распознавателя), но помимо перехода автомата в состояние q’ при входном символе х и верхнем символе в магазине у и записи в магазин цепочки z*, на выходную ленту выдается операционная цепочка W*.
Процедура для построения нисходящего и восходящего МП преобразователей по простой схеме СУ-перевода для синтаксического анализа определяется следующими теоремами.
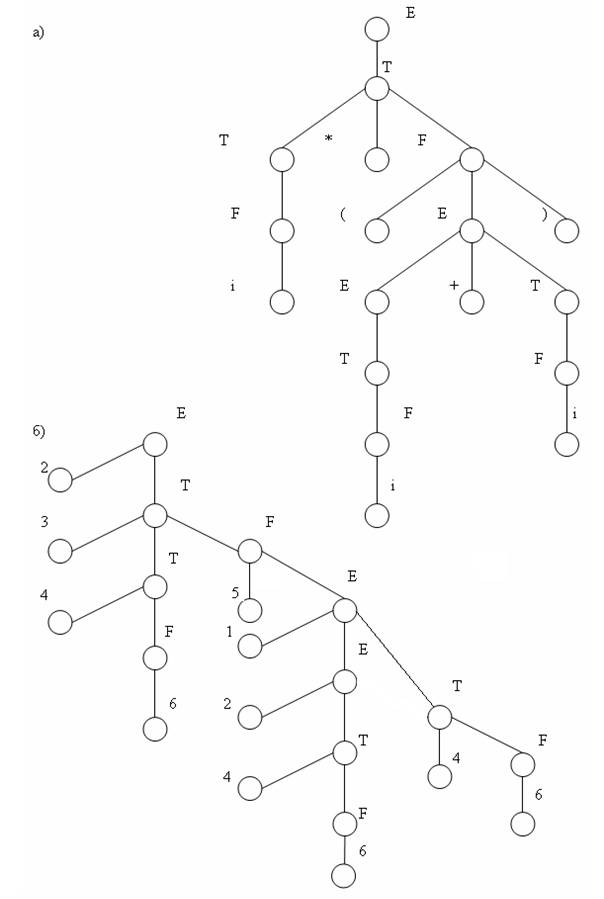
Рис. 3.18. Перевод цепочки i*(i+i) СУ-схемой: а – вход СУ схемы; б – выход СУ схемы
Теорема 3.5.1. [4] Пусть G = <N, T, P, S> — КС-грамматика в нормальной форме Грейбах, в которой правила пронумерованы числами 1, 2, …, р, и М = <Q, A, ![]() , Г,
, Г, ![]() , q0, z0, F> — расширенный недетерминированный МП-преобразователь, у которого:
, q0, z0, F> — расширенный недетерминированный МП-преобразователь, у которого:
1) A = T![]() {
{ ![]() };
};
2) Q = {q};
3) Г = N![]() T
T![]() {#};
{#};
4) ![]() = {1, 2, …, p};
= {1, 2, …, p};
5) q0 = q;
6) z0 = #S;
7) F =![]() ;
;
8) (q, a, A) = ![]() (q,
(q, ![]() , i), если (A
, i), если (A![]() a
a![]() )
)![]() P с номером i;
P с номером i;
9) ![]() (q, b, b) = (q,
(q, b, b) = (q,![]() ,
,![]() ) для всех b
) для всех b![]() T и (A
T и (A![]() b
b![]() )
)![]() P;
P;
10) ![]() (q,
(q, ![]() , #) = (ДОПУСТИТЬ,
, #) = (ДОПУСТИТЬ,![]() ,
,![]() );
);
11) ![]() (q, x, y) = (ОТВЕРГНУТЬ,
(q, x, y) = (ОТВЕРГНУТЬ,![]() ,
,![]() ) для всех ситуаций, не перечисленных в п.п. 8 – 10.
) для всех ситуаций, не перечисленных в п.п. 8 – 10.
Тогда недетерминированный МП-преобразователь М является функциональным интерпретатором простой схемы СУ-перевода
D = <N, T![]() {1, 2, …, p}, R, S>
{1, 2, …, p}, R, S>
для левого (нисходящего) анализа цепочек языка, порождаемого входной грамматикой.
Данная теорема утверждает, что если входная цепочка символов является допустимой в грамматике G, то на выходе построенного указанным образом МП-преобразователя будет выдана последовательность номеров подстановок из множества Р, которая отвечает левому выводу входной цепочки.
Пример 3.5.2. Пусть D = <{S, L’, L, I}, {real, , , i}, {1, 2, 3, 4, 5, 6}, S = {S}> – простая СУ-схема перевода с правилами R:
1) S![]() real L’, I L’;
real L’, I L’;
2) L’![]() i L, 2 L;
i L, 2 L;
3) L’![]() i, 3;
i, 3;
4) L![]() , I L, 4 I L;
, I L, 4 I L;
5) L![]() , I, 5 I;
, I, 5 I;
6) L![]() i, 6.
i, 6.
МП-преобразователь для данной простой СУ-схемы имеет компоненты:
A = {real, i, , , ![]() };
};
Q = {q};
Г = {S, L’, L, I, real, , , i, #};
![]() = {1, 2, 3, 4, 5, 6}; F =
= {1, 2, 3, 4, 5, 6}; F = ![]() ; z0 = #S; q0 = q; и
; z0 = #S; q0 = q; и
![]() (q, real, S) = (q, L’, 1);
(q, real, S) = (q, L’, 1);
![]() (q, i, L’) = (q, L, 2);
(q, i, L’) = (q, L, 2);
![]() (q, i, L’) = (q,
(q, i, L’) = (q, ![]() , 3);
, 3);
![]() (q, , , L) = (q, I L, 4);
(q, , , L) = (q, I L, 4);
![]() (q, , , L) = (q, I, 5);
(q, , , L) = (q, I, 5);
![]() (q, , , I) = (q, I, 6);
(q, , , I) = (q, I, 6);
![]() (q,
(q, ![]() , #,) = (ДОПУСТИТЬ,
, #,) = (ДОПУСТИТЬ, ![]() ,
, ![]() );
);
![]() (q, x, y,) = (ОТВЕРГНУТЬ,
(q, x, y,) = (ОТВЕРГНУТЬ, ![]() ,
, ![]() ).
).
Последовательность конфигураций МП-преобразователя при переводе цепочки real i, i ![]() следующая:
следующая:
|
СОСТОЯНИЕ |
МАГАЗИННАЯ ПАМЯТЬ |
ВХОДНАЯ ЛЕНТА |
ВЫХОДНАЯ ЛЕНТА |
|
q |
#S |
real i, i |
|
|
q |
#L’ |
i, i |
1 |
|
q |
#L |
, i |
12 |
|
q |
#I |
i |
125 |
|
q |
# |
|
1256 |
|
ДОПУСТИТЬ |
Процедура построения восходящего МП-преобразователя определяется следующей теоремой:
Теорема 3.5.2. [4] Пусть G = <N, T, P, S> – КС-грамматика в нормальной форме Грейбах, в которой правила занумерованы числами 1, 2, …, р, и M = <Q, A, ![]() , Г,
, Г, ![]() , q0, z0, F> – расширенный восходящий МП-преобразователь, компоненты которого определяются следующим образом:
, q0, z0, F> – расширенный восходящий МП-преобразователь, компоненты которого определяются следующим образом:
1) A = T![]() {
{![]() };
};
2) Q = {q};
3) Г = N![]() T
T![]() {#};
{#};
4) ![]() = {1, 2, …, p};
= {1, 2, …, p};
5) q0 = q;
6) z0 = #;
7) F = ![]() ;
;
8) Функция ![]() определяется по следующим правилам:
определяется по следующим правилам:
а) (q, A, i)![]()
![]() (q,
(q, ![]() ,
,![]() ), если (A
), если (A![]()
![]() )
)![]() P с номером i;
P с номером i;
б) ![]() (q, a,
(q, a,![]() ) = (q, a,
) = (q, a,![]() ) для всех a
) для всех a![]() T;
T;
в) ![]() (q,
(q, ![]() , #S) = (ДОПУСТИТЬ,
, #S) = (ДОПУСТИТЬ, ![]() ,
,![]() );
);
г) ![]() = (q, x, y,) = (ОТВЕРГНУТЬ,
= (q, x, y,) = (ОТВЕРГНУТЬ, ![]() ,
, ![]() ) для всех ситуаций, не перечисленных в п.п. а) — в).
) для всех ситуаций, не перечисленных в п.п. а) — в).
Пример 3.5.3. Восходящий МП-преобразователь для простой СУ-схемы из примера 3.5.2 имеет следующее описание:
A = {real, i, , , ![]() };
};
Q = {q};
Г = {S, L’, L, I, real, , , i, #};
![]() = {1, 2, 3, 4, 5, 6};
= {1, 2, 3, 4, 5, 6};
z0 = #;
q0 = q;
![]() = (q,
= (q, ![]() , real, L’) = (q, S, 1);
, real, L’) = (q, S, 1);
![]() = (q,
= (q, ![]() , iL) = (q, L’, 2);
, iL) = (q, L’, 2);
![]() = (q,
= (q, ![]() , i) = (q, L’, 3);
, i) = (q, L’, 3);
![]() = (q,
= (q, ![]() , , I L) = (q, L, 4);
, , I L) = (q, L, 4);
![]() = (q,
= (q, ![]() , , I) = (q, L, 5);
, , I) = (q, L, 5);
![]() = (q,
= (q, ![]() , i) = (q, I, 6);
, i) = (q, I, 6);
![]() = (q, real,
= (q, real,![]() ) = (q, real,
) = (q, real,![]() );
);
![]() = (q, , ,
= (q, , ,![]() ) = (q, , ,
) = (q, , ,![]() );
);
![]() = (q, i,
= (q, i,![]() ) = (q, i,
) = (q, i,![]() );
);
![]() = (q,
= (q, ![]() , #S,) = (ДОПУСТИТЬ,
, #S,) = (ДОПУСТИТЬ, ![]() ,
, ![]() );
);
![]() = (q, x, y,) = (ОТВЕРГНУТЬ,
= (q, x, y,) = (ОТВЕРГНУТЬ, ![]() ,
, ![]() ).
).
Последовательность конфигураций МП-преобразователя при переводе цепочки real i, i ![]() следующая:
следующая:
|
СОСТОЯНИЕ |
МАГАЗИННАЯ ПАМЯТЬ |
ВХОДНАЯ ЛЕНТА |
ВЫХОДНАЯ ЛЕНТА |
|
q |
# |
real i, i |
|
|
q |
# real |
i, i |
|
|
q |
# real i |
, i |
|
|
q |
# real i, |
i |
|
|
q |
# real i, i |
|
6 |
|
q |
# real i, I |
|
65 |
|
q |
# real iL |
|
652 |
|
q |
# real L’ |
|
6521 |
|
q |
# S |
|
6521 |
|
ДОПУСТИТЬ |
# |
|
6521 |
Простые СУ-схемы перевода являются хорошей моделью компилятора, в которой синтаксический анализ и генерация выходного кода объединены в одну фазу. В такой модели операции генерации кода (в СУ-схеме перевода им соответствуют операционные символы или символы действий) совмещены с операциями разбора. При моделировании такого СУ-перевода с помощью МП-преобразователя важную роль играет детерминированность разбора. Это связано, в первую очередь, не столько со сложностью перебора альтернативных правил вывода и реализации механизма возвратов в случае неуспешных выводов, сколько с необходимостью отмены выполненных действий по генерации кода в случае возвратов. Поэтому немаловажным является выяснение того, какие виды простых СУ-переводов могут выполняться на детерминированном МП-преобразователе. Ответ на данный вопрос дают следующие теоремы.
Теорема 3.5.3. [5] Пусть D = (Т,![]() , N, R, S) простая СУ-схема, входной грамматикой которой служит LL(К)-грамматика. Тогда СУ-перевод {(х, у) | (х, у)
, N, R, S) простая СУ-схема, входной грамматикой которой служит LL(К)-грамматика. Тогда СУ-перевод {(х, у) | (х, у)![]()
![]() (D)} можно осуществить детерминированным МП-преобразователем.
(D)} можно осуществить детерминированным МП-преобразователем.
Данная теорема, no-существу, утверждает, что если для входной грамматики СУ-схемы можно построить детерминированный нисходящий МП-преобразователь, то и любой простой СУ-перевод можно реализовать с помощью детерминированного МП-преобразователя. Для построения детерминированного нисходящего МП-преобразователя можно воспользоваться правилами построения детерминированного МП-распознавателя, описанными в п. 3.3, доопределив соответствующие команды операциями выдачи символов действий на выходную ленту, интерпретируя их как вызовы процедур, реализующих генерацию выходного кода компилятора.
Несколько иначе дело обстоит с моделированием СУ-перевода с помощью детерминированного восходящего МП-преобразователя. Восходящий детерминированный перевод применим не для произвольных СУ-схем, а лишь для СУ-схем определенного вида.
Определение 3.5.3. СУ-схему D = (Т,![]() , N, R, S) будем называть постфиксной, если каждое правило из R имеет вид А
, N, R, S) будем называть постфиксной, если каждое правило из R имеет вид А![]()
![]() ,
,![]() , где
, где ![]()
![]() N*
N*![]() *. Иными словами, каждый элемент перевода представляет собой цепочку из нетерминалов, за которой следует цепочка выходных символов.
*. Иными словами, каждый элемент перевода представляет собой цепочку из нетерминалов, за которой следует цепочка выходных символов.
Теорема 3.5.4. [5] Пусть D = (Т, ![]() , N, R, S) простая постфиксная СУ-схема, входной грамматикой которой служит LR(К)-грамматика. Тогда перевод {(х, у) | (x, у)
, N, R, S) простая постфиксная СУ-схема, входной грамматикой которой служит LR(К)-грамматика. Тогда перевод {(х, у) | (x, у)![]()
![]() (D)} можно осуществить детерминированным МП-преобразователем.
(D)} можно осуществить детерминированным МП-преобразователем.
Построение детерминированного МП-преобразователя для постфиксного CУ-перевода не вызывает больших трудностей, если пользоваться правилами построения
восходящего МП-распознавателя, приведенными в п. 3.4.
Если же грамматика простой СУ-схемы перевода является LR(К)-грамматикой, а СУ-схема не является постфиксной, то такой перевод все же может быть реализован. Один из возможных методов состоит в использований многопроходной схемы перевода [5]. Рис. 3.19 [5] иллюстрирует каскадную связь ДМП-преобразователей. Поясним данную схему.
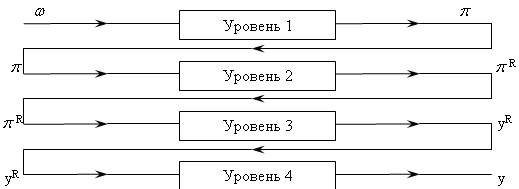
Рис. 3.19. Простой СУ-перевод над LR(K) – грамматикой
Пусть D = <Т, ![]() , N, R, S> — простая не постфиксная СУ-схема с входной LR(K)-грамматикой G. Первый уровень многопроходного перевода — восходящий ДМП-преобразователь, реализующий СУ-перевод для синтаксического анализа: входная цепочка
, N, R, S> — простая не постфиксная СУ-схема с входной LR(K)-грамматикой G. Первый уровень многопроходного перевода — восходящий ДМП-преобразователь, реализующий СУ-перевод для синтаксического анализа: входная цепочка ![]()
![]() преобразуется в цепочку
преобразуется в цепочку ![]() -последовательность номеров правил, участвующих в правом разборе. На втором уровне осуществляется обращение
-последовательность номеров правил, участвующих в правом разборе. На втором уровне осуществляется обращение ![]() — получается обратный вывод
— получается обратный вывод ![]() R.
R.
Входом третьего уровня является цепочка ![]() R. Выходом – перевод, определяемый простой СУ–схемой D’ = <T’,
R. Выходом – перевод, определяемый простой СУ–схемой D’ = <T’, ![]() , N, R’, S>, где R’ содержит правило A
, N, R’, S>, где R’ содержит правило A![]() iBmBm-1 B1, ymBm …y1B1y0 тогда и только тогда, когда A
iBmBm-1 B1, ymBm …y1B1y0 тогда и только тогда, когда A![]() x0B1x1 …Bmxm, y0B1 …Bmym только правило из R, a A
x0B1x1 …Bmxm, y0B1 …Bmym только правило из R, a A![]() x0B1 …Bmym – правило с номером I входной LR(K)-грамматики. D’ – простая СУ схема, основанная на LL(1)-грамматике, у которой входными терминальными символами являются номера правил подстановки, которые применялись на первом уровне при выводе цепочки
x0B1 …Bmym – правило с номером I входной LR(K)-грамматики. D’ – простая СУ схема, основанная на LL(1)-грамматике, у которой входными терминальными символами являются номера правил подстановки, которые применялись на первом уровне при выводе цепочки ![]()
![]() . Таким образом, третий уровень – нисходящий ДМП-преобразователь. На четвертом уровне просто обращается выход третьего.
. Таким образом, третий уровень – нисходящий ДМП-преобразователь. На четвертом уровне просто обращается выход третьего.
Необходимо отметить, что LR(K) разбор хотя и применим к более широкому классу языков, чем LL(K) разбор, но при реализации детерминированных непостфиксных СУ-переводов LR(K) разбор уступает LL(K) разбору.
Рассмотренная выше модель синтаксического анализатора как СУ-перевода текста исходной программы в цепочку номеров правил в правом или левом разборе, позволяет легко заменить номера правил процедурами (командами) построения синтаксического дерева программы.
Синтаксическое дерево программы — это синтаксическое дерево вывода с удаленными цепочками цепных правил. В синтаксическом дереве программы внутренние вершины в основном соответствуют операциям, а листья — операндам. Физическое представление синтаксического дерева программы называют обычно промежуточной программой.
Пример 3.5.4. На рис. 3.20, а показано синтаксическое дерево вывода цепочки а+b*с+d в грамматике простых арифметических выражений из примера 3.4.3 (терминальному символу i в грамматике соответствуют символы а, b, с, d
цепочки). На рис. 3.20, б приведено синтаксическое дерево программы этой же цепочки, построенной на основе ее дерева вывода.
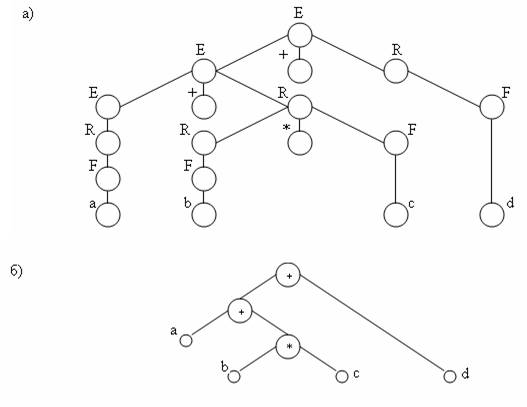
Рис. 3.20. Синтаксические деревья: а – вывода; б – программы
В простейшем случае последовательности номеров правил правого или левого разбора можно считать промежуточными программами.