Рассмотрим антисипативный способ начисления сложных процентов.
В формулах, приведенных ниже, применены следующие обозначения:
dc (%) – сложная годовая учетная ставка;
dc – относительная величина сложной учетной ставки;
kН.У – коэффициент наращения для случая учетной ставки;
f – номинальная годовая учетная ставка.
По прошествии первого года наращенная сумма S1 в соответствии с формулой (3.20) составит:
![]() .
.
Через год данная формула будет применяться к сумме S1:
![]()
и далее, аналогично случаю сложных ставок ссудных процентов. После n лет наращенная сумма составит:
![]() . (3.41)
. (3.41)
Для множителя наращения получаем формулу
![]() . (3.42)
. (3.42)
Сравнение формул (3.25) и (3.41) показывает, что при равенстве ссудного процента и учетной ставки наращение первоначальной суммы во втором случае происходит интенсивнее. Поэтому в экономической литературе часто можно встретить утверждение, что декурсивный метод начисления более выгоден для заемщика, а антисипативный – для кредитора. С ростом процентной ставки разница в величине наращенной суммы становится огромной, и сравнение двух методов — с точки зрения выгодности – утрачивает смысл.
Как и при декурсивном способе, возможны различные варианты начисления антисипативных процентов. Им соответствуют формулы, полученные соответствующим образом. Так, для периода начисления, не являющегося целым числом, имеем:
![]() . (3.43)
. (3.43)
При учетной ставке, изменяющейся в течение срока ссуды, наращенная сумма рассчитывается по формуле
![]() , (3.44)
, (3.44)
где n1, n2, …, nN – продолжительность интервалов начисления в годах;
d1, d2, …, dN – учетные ставки, соответствующие данным интервалам.
Для начисления процентов m раз в году формула принимает следующий вид:
![]() (3.45)
(3.45)
или
![]() , (3.46)
, (3.46)
где mn – целое число интервалов начисления за весь период начисления;
l – часть интервала начисления.
При непрерывном начислении процентов наращенная сумма рассчитывается по формуле:
![]() . (3.47)
. (3.47)
Путем преобразования формул (3.41) – (3.47) получаем формулы для нахождения первоначальной суммы, срока начисления и величины учетной ставки:
![]() ; (3.48)
; (3.48)
![]() ; (3.49)
; (3.49)
![]() ; (3.50)
; (3.50)
![]() ; (3.51)
; (3.51)
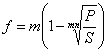 . (3.52)
. (3.52)
Чтобы выбрать в каждом конкретном случае наиболее выгодную процентную ставку, не обязательно просчитывать получаемые суммы, на практике можно воспользоваться эквивалентными процентными ставками.