Самым распространенным способом моделирования тенденций временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени.
Длительную тенденцию изменения показателей временного ряда, на которую могут налагаться другие составляющие, называют «тренд».
Временной ряд содержит результаты наблюдения за процессом на некотором интервале времени, называемом участком наблюдения (рис. 3.8). Отрезок времени от последнего наблюдения до того момента, для которого нам необходимо получить прогноз, называется участком упреждения.
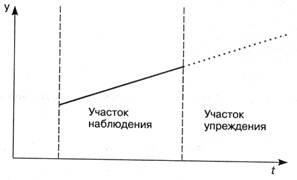
Рис. 3.8 Прогноз экстраполяцией тренда
Сплошная линия (участок наблюдения) изображает тренд. Математическая модель тренда построена на основе данных временного ряда (точки вдоль тренда). Пунктирная линия характеризует прогнозные значения экстраполированной линии тренда.
Некоторые социально-экономические процессы и объекты моделируются на основе тренда с помощью определенных функций.
Временные ряды наблюдаемых показателей чаще всего аппроксимируются следующими элементарными функциями: ![]() (уравнение прямой линии);
(уравнение прямой линии); ![]() (парабола 2-го порядка);
(парабола 2-го порядка); ![]() (логарифмическая);
(логарифмическая); ![]() (степенная);
(степенная); ![]() (показательная);
(показательная); ![]() (гиперболическая); у=1: (а + b х еt ) (логистическая); у = sin t и у=cos t (тригонометрическая). Возможно использование комбинированных функций.
(гиперболическая); у=1: (а + b х еt ) (логистическая); у = sin t и у=cos t (тригонометрическая). Возможно использование комбинированных функций.
Методы экстраполяции динамических рядов (трендовые методы) делятся на два основных блока методов: аналитические и адаптивные (рис. 3.9).
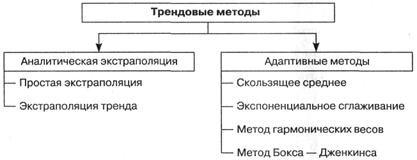
Рис. 3.9 Методы экстраполяции динамических рядов
При простой экстраполяции динамического ряда прогнозная оценка (точечный прогноз) на период упреждения рассчитывается как средняя арифметическая значений интервала оценивания.
Прогнозирование на основе экстраполяции тренда включает ряд последовательных этапов:
- анализ и обработка исходной информации, проверка ряда динамики на наличие тренда;
- выбор вида функции, описывающей временной ряд;
- определение параметров прогнозной функции;
- расчет точечных и интервальных прогнозов.
Выделение тренда может быть произведено тремя методами: скользящей средней, укрупнения интервалов или аналитического выравнивания.
Под аналитическим выравниванием, которое используется наиболее часто, подразумевается определение основной проявляющейся во времени тенденции развития изучаемого явления.
Параметры каждого из перечисленных выше трендов можно определить методом наименьших квадратов (МНК), используя в качестве независимой переменной время t=1,2,…,n, а в качестве зависимой переменной — фактические уровни временного ряда уt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Выбранная прогнозная эмпирическая функция, описывающая динамический ряд, должна минимизировать стандартное отклонение S на интервале оценивания, обеспечивать тесноту связи (по коэффициенту корреляции); аппроксимирующее уравнение должно быть адекватно фактической временной тенденции (по F-критерию) и устранять автокорреляцию.
Оценка адекватности может проводиться с помощью следующих показателей.
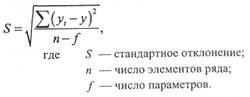
![]()
средняя ошибка аппроксимации.
А < 12% свидетельствует об адекватности функции реальным условиям.
![]()
коэффициент детерминации.
![]() — остаточная сумма квадратов отклонений фактических значений от расчетных.
— остаточная сумма квадратов отклонений фактических значений от расчетных.
R2 (квадрат коэффициента корреляции) — доля дисперсии, объясняемая регрессией, в общей дисперсии результативного признака.
F-тест — оценивание качества уравнения — состоит в проверке гипотезы H0 о статистической незначимости уравнения регрессии и показателя тесноты связи.
![]()
F-критерий Фишера.
Наличие автокорреляции остатков выявляется критерием даром Уотсона (DW):
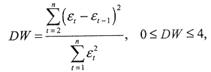
где![]()
Рассмотрим последовательность составления прогнозной модели на примере расчета среднесписочной численности занятых в промышленности (табл. 3.8).
Таблица 3.8
Среднесписочная численность промышленно-производственного персонала
|
Год |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
|
Численность |
194,8 |
194,5 |
192,9 |
189,8 |
189,2 |
185,6 |
180,4 |
180,5 |
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Численность |
166,8 |
155,5 |
146,8 |
133,4 |
131,2 |
124,5 |
122,3 |
117,8 |
Динамический ряд численности занятых в промышленности имеет явно выраженную тенденцию к убыванию и описывается линейной функцией (рис.)3.10.
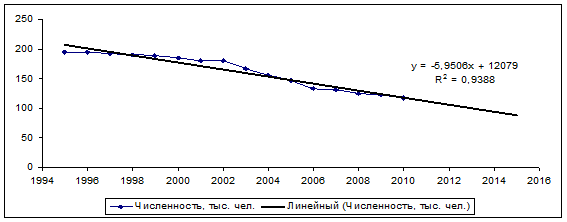
Рис. 3.10 Численность персонала и ее линейный тренд
Прогнозирование среднесписочной численности промышленно-производственного персонала на 5 лет, до 2015 г. проведено на основе уравнения прямой линии, с помощью программы EXCEL, анализ данных. Получено уравнение связи ![]() , где Y – численность промышленно-производственного персонала, x – порядковый номер года. Уравнение адекватно, модель является достоверной, так как коэффициент детерминации
, где Y – численность промышленно-производственного персонала, x – порядковый номер года. Уравнение адекватно, модель является достоверной, так как коэффициент детерминации ![]() =0,9388 больше 0,65.
=0,9388 больше 0,65.
Подставив в уравнение связи вместо х числа от 2011 до 2015, рассчитаем прогнозные значения численности персонала (табл. 3.9).
Таблица 3.9
Прогнозные оценки среднесписочной численности промышленно-производственного персонала региона на период 2011-2016 гг., тыс. чел.
|
2011 |
2012 |
2013 |
2014 |
2015 |
|
113,55 |
107,6 |
101,65 |
95,7 |
89,75 |
К адаптивным методам относятся: методы скользящей средней, экспоненциального сглаживания, гармонических весов, авторегрессий и метод Бокса — Дженкинса. Параметры адаптивных моделей чаще всего рассчитываются с использованием пакетов прикладных программ Statistica, SPSS или Forecast Expert.
Выделение тренда с помощью скользящих средних
Метод скользящих средних позволяет «сгладить» ряд значений с тем, чтобы выделить тренд. При использовании этого метода берется среднее (обычное среднеарифметическое) фиксированного числа значений. Затем это вычисление повторяется по всему ряду значений. Полученные скользящие средние обозначат общий тренд временного ряда. Число значений, которое используется при вычислении среднего, определяет результат сглаживания. В целом, чем больше точек берется, тем сильнее сглаживаются данные.
Сгладим с помощью скользящих средних колебания объемов продаж на временных промежутках. Например, в нижеприведенной таблице 3.10 представлены исходные данные об объемах продаж, а также скользящие средние, рассчитанные по каждым 3 (трем) значениям (так называемые трехточечные скользящие средние).
Таблица 3.10
Годовой объем продаж компании и трехточечные скользящие средние
|
Год |
Годовой объем продаж, млн. руб. |
Трехточечные скользящие средние, млн. руб. |
|
1997 |
170 |
|
|
1998 |
120 |
131, 67 |
|
1999 |
105 |
127,00 |
|
2000 |
156 |
150,00 |
|
2001 |
189 |
150,67 |
|
2002 |
107 |
154,33 |
|
2003 |
167 |
159,67 |
|
2004 |
205 |
183,33 |
|
2005 |
178 |
179,67 |
|
2006 |
156 |
174,33 |
|
2007 |
189 |
193,33 |
|
2008 |
235 |
209,00 |
|
2009 |
203 |
235,00 |
|
2010 |
267 |
236,33 |
|
2011 |
239 |
Эти скользящие средние рассчитаны следующим образом. Первые три значения объема продаж (за 1997—1999 гг.) складываются, а затем делятся на три, получаем значение первого скользящего среднего: (170 + 120 + 105)/3 = 395/3=131,67
Это значение записывается по центру значений, по которым рассчитывалось среднее значение, и поэтому в таблице значение скользящего среднего, полученное первым, стоит против 1998 г. Следующее значение скользящего среднего рассчитывается так:
Второе скользящее среднее =(120 +105 +156)/3=381/3= 127
Далее проводим аналогичные вычисления по трем значениям вплоть до последнего набора значений за 2009—2011 гг., где значение скользящего среднего равно 236,33.
На рис. 3.11 показано, как трехточечные скользящие средние существенно сгладили график. Были сняты многие колебания исходных данных, и полученный набор значений более четко показывает тренд данных. Таким образом, можно делать прогнозы исходя из оценок линии регрессии, составленной по значениям скользящих средних. Однако трехточечные скользящие средние все еще выказывают некоторые колебания. Ряд можно сгладить еще больше, если увеличить число точек при вычислении значений. Например, пяти-, семиточечные скользящие средние.
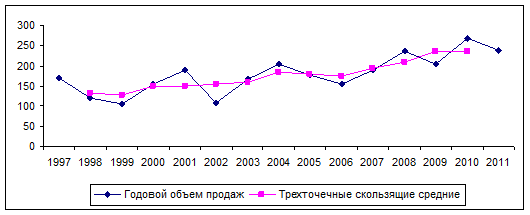
Рис. 3.11 Объемы продаж компании и скользящие средние, млн. руб.