Метод Гаусса-Жордана – это модификация метода Гаусса. После выполнения прямого хода в методе Гаусса-Жордана матрица преобразуется к диагональной, а не к верхней треугольной. Обратный ход в методе Гаусса-Жордана – это решение системы линейных уравнений с диагональной матрицей.

Рассмотрим пример использования метода Гаусса-Жордана.

Пример

Используя метод Гаусса-Жордана с частичным выбором ведущего элемента, решить систему линейных уравнений:

Решение

Прямой ход

Находим максимальный по модулю элемент в непреобразованном столбце и меняем местами строки. Получим:

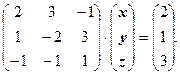
Умножим первое уравнение на (-0.5) и прибавим ко второму. Умножим первое уравнение  на (0.5) и прибавим к третьему. Получим:

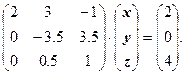
Выбираем максимальный по модулю элемент в непреобразованном столбце, он равен , поэтому перестановка строк не нужна. Теперь нам нужно занулить не только , но и . Умножим второе уравнение на 6/7 и прибавим к первому. Умножим второе уравнение на 1/7 и прибавим к третьему. Получим:

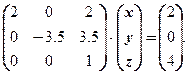
Третье уравнение умножим на (-3.5) и прибавим ко второму. Третье уравнение умножим на (-2) и прибавим к первому. Получим:

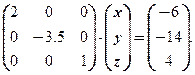
Прямой ход метода Гаусса-Жордана закончен.

Обратная подстановка

z = 4.

-3.5y = -14, следовательно, y = 4.

2x = -6, следовательно, x = -3.