Пусть ищется решение системы линейных уравнений  с невырожденной матрицей  A ().

Так как , следовательно, система линейных уравнений  имеет единственное решение.

Преобразуем систему линейных уравнений  к виду: , где  – квадратная матрица,  – вектор. Причем системы являются эквивалентными, то есть их решения совпадают. В дальнейшем мы будем рассматривать систему .

Выбирается вектор начального приближения:

.

Строится итерационный процесс:

.

Итерационный процесс прекращается при выполнении условия:

,

где  – точное решение системы линейных уравнений. В этом случае  – приближенное решение системы линейных уравнений с точностью , полученное методом итераций.

Естественно, возникает ряд вопросов:

· При каких условиях последовательность  сходится к точному решению системы линейных уравнений?

· Как выбирать начальное приближение ?

· Как сформулировать условия остановки итерационного процесса?

Последовательно будем отвечать на эти вопросы.

Теорема о сходимости

Пусть система линейных уравнений  имеет единственное решение. Для сходимости последовательности приближений  к точному решению системы линейных уравнений  достаточно, чтобы . При выполнении этого условия последовательность  сходится к точному решению при любом векторе начального приближения .

Оценка погрешности. Для метода итераций удается получить две оценки погрешности: априорную и апостериорную.

Априорная оценка погрешности – это оценка погрешности , которую можно получить до начала вычислений, зная только  и .

Апостериорная оценка погрешности – это оценка погрешности , которую получают, используя вычислительные приближения   и зная .

Теорема (априорная оценка погрешности)

Пусть система линейных уравнений  имеет единственное решение. Пусть . Тогда имеет место неравенство:

,   ,

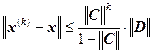где  – k-е приближение, полученное методом итераций;  – точное решение системы линейных уравнений .

Отметим, что априорная оценка погрешности позволяет до вычислений оценить число шагов k, необходимых для достижения точности :

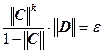,        ,  следовательно, .

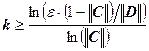Следствие. Пусть система линейных уравнений  имеет единственное решение. Пусть , тогда для числа итераций k, необходимых для достижения точности e, справедливо следующее неравенство:

.

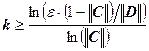Отметим, что все нормы, входящие в это неравенство, должны быть согласованы. То есть если мы выбираем первую норму матрицы С, то должны взять и первую норму вектора D. Как правило, число шагов k, полученное из этой оценки, является заметно завышенным.

Теорема (апостериорная оценка погрешности)

Пусть система линейных уравнений  имеет единственное решение. Пусть , тогда имеет место неравенство:

. 

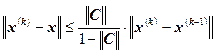Следствие. Если выполняется условие , то . То есть, для того чтобы получить приближенное решение с точностью e, необходимо использовать следующее условие остановки итерационного процесса:

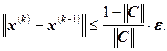
Сформулируем алгоритм метода итераций

1) Задана система линейных уравнений с невырожденной матрицей. Преобразуем систему линейных уравнений  к виду: , где C – квадратная матрица, D – вектор. Причем системы являются эквивалентными и .

2) Выбираем произвольный вектор начального приближения:   .

3) Строим последовательность:   .

4) Эта последовательность сходится к точному решению системы линейных уравнений . При выполнении условия остановки итерационного процесса вычисления прекращаются.

Пример 1

Построить и обосновать алгоритм решения системы линейных уравнений  методом итераций с точностью :

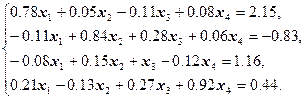
Решение

Прежде всего, необходимо обосновать, что , если это не заданно в условии задачи. В нашем случае можно воспользоваться следующей теоремой:

Теорема

Если для матрицы А выполняются n неравенств 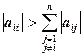 , то   матрица А невырожденная. 

Это свойство называется диагональным преобладанием: модуль диагонального элемента больше, чем сумма модулей внедиагональных элементов строки.

Эту теорему можно сформулировать и в другом виде, используя перенумерацию строк (столбцов). Определитель матрицы А не равен нулю, если в каждой строке (столбце) А имеется преобладающий элемент и эти элементы расположены в различных столбцах (строках).

В нашем случае:

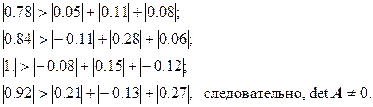
В общем случае, нахождение матрицы C – сложная задача. Но в нашем примере очень легко найти матрицу C, удовлетворяющую всем условиям. Достаточно взять , тогда :

,             – эти системы эквивалентны.

.

Найдем С и докажем, что :

.

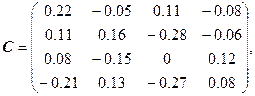
Вычислим первую норму С:

2. Выбираем вектор начального приближения:

Так как , то итерационный процесс:  сходится для любого     начального приближения.

3. Формула метода: .

4. Условие остановки итерационного процесса:

;

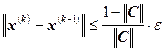, следовательно, .

При выполнении этого условия  считается приближенным решением система линейных уравнений с точностью , полученным методом итераций.

Пример 2

Оценить число шагов, необходимых для достижения точности , при решении системы линейных уравнений  методом итераций.

Решение

Рассмотрим ту же систему линейных уравнений. Воспользуемся следствием из априорной оценкой погрешности. Условие на матрицу C выполнено:

, следовательно, метод итераций сходится и справедливо неравенство:

.

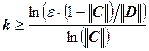Мы вычисляли первую норму матрицы С, следовательно, и у вектора D также необходимо вычислять первую норму:

,

,

следовательно, .

Оценку сложности алгоритма метода итераций (по времени) мы получаем из априорной оценки погрешности

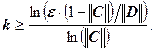
На каждом шаге итерационного процесса мы выполняем О(n²) арифметических действий, где n – порядок матрицы, следовательно, общее число арифметических действий: kО(n²).

Для реализации алгоритма метода итераций на каждом шаге необходимо хранить матрицу С, ,  и D, следовательно, требуется памяти О(n²).

Если ||C|| < 1, то алгоритм метода итераций для решения система линейных уравнений является устойчивым по отношению к вычислительной погрешности.

Недостатки метода итераций для решения систем линейных уравнений

1) Нет общего приема для перехода от матрицы А к матрице С таким образом, чтобы .

2) Метод итераций медленно сходится, если  близка к 1.