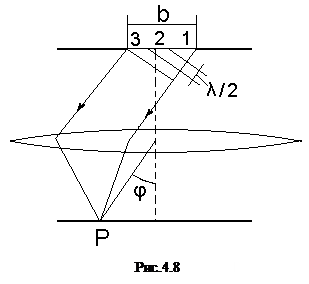
Пусть плоская монохроматическая волна падает нормально плоскости узкой щели шириной b (рис. 4.8). На экране в фокальной плоскости линзы собираются параллельные пучки, образующие дифракционную картину. Оптическая разность хода между крайними лучами, идущими от щели в произвольном направлении j равна:

.

Разобьем открытую часть волновой поверхности в плоской щели на зоны Френеля, имеющие вид полос, параллельных ребру щели (на нашем рисунке получилось три зоны Френеля).  Ширина каждой зоны должна быть такой, чтобы разность хода от краев этих зон до экрана равнялась l2, следовательно, число зон Френеля равно: Z = D/(l¤2). При наложении световых волн от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно погашают друг друга.

Если число зон Френеля четное (Z = 2m, где m = 1, 2, 3…), то будет наблюдаться минимум, т.е. условие минимума имеет вид:

.

При нечетном числе зон Френеля () наблюдается максимум, условие которого имеет вид:

.

Таким образом, наличие максимума или минимума определяется только разностью хода крайних лучей, хотя в точку наблюдения приходят волны от каждой точки открытой части волновой поверхности. Интенсивность центрального и последующих максимумов относятся как 1 : 0,047 : 0,017 : 0,0083, т.е. основная часть света сосредоточена в центральном максимуме.

Поскольку положение дифракционных максимумов зависит от длины волны, в белом свете центральный максимум дифракционной картины имеет вид белой полосы, а боковые максимумы радужно окрашены.