Задача о Кенигсбергских мостах (Эйлер, 1736 г.). На рисунке 4.1 слева изображена часть реки Прейгель, находящейся  в Кенигсберге (ныне Калининграде). Требуется найти маршрут пешехода, проходящий через все мосты. Через каждый мост пешеход должен пройти ровно один раз. Эйлер доказал, что эта задача не имеет решений.

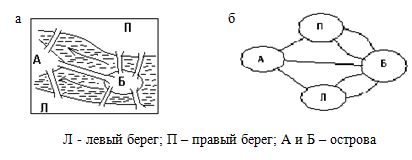
4.1. Схема мостов (а) и соответствующий ей граф (б)

Сначала напомним определение простого графа, приведенное в подразделе 1.5. Для произвольного множества V обозначим через P₂(V) множество, состоящее из подмножеств {v₁,v₂} Í V,  каждое из которых состоит из двух не равных между собой элементов.

Определение 1

Простым (неориентированным) графом G = (V,E) называется пара, состоящая из множества V и произвольного подмножества E Í P₂(V). Элементы из V называются вершинами, а из E – ребрами.

Вершины простого графа изображаются как точки или круги, а ребра – как отрезки.

Обобщим определение простого графа.

Определение 2

Графом называется тройка  (V, E, a), состоящая из множеств V, E и функции a: E ®P₂(V), сопоставляющей каждому eÎE неупорядоченную пару {u,v}. Элементы из E называются ребрами,  элементы из V – вершинами.

Если a(e)={u,v}, то  вершины u и v называются концами ребра e.  В этом случае u и v называются смежными вершинами, инцидентными ребру e. Если концы ребра e равны (a(e) состоит из единственного элемента),  то ребро e называется петлей.

Степенью вершины v называется число инцидентных ей ребер. Ребро, являющееся петлей, учитывается два раза. В частности, петля дает степень 2. Для графа, соответствующего схеме Кенигсбергских мостов, степени вершин равны 3, 3, 3 и 5. Путем в

графе называется последовательность вершин и ребер v₀g₁v₁g₂v₂ … v_n-1g_nv_n, таких что v_i и v_i+1 инцидентны ребрам g_i+1 для всех i Î {1,2, …, n}.

Граф, допускающий путь, не содержащий кратных ребер и содержащий все ребра, называется эйлеровым. Такой путь тоже называется эйлеровым.

На рис. 4.1, б изображен граф, ребра которого соответствуют мостам, а вершины – частям суши. Задача о Кенигсбергских мостах имеет решение тогда и только тогда, когда этот граф является эйлеровым.

Теорема

Граф является эйлеровым тогда и только тогда, когда нечетную степень имеют не более двух вершин.

Доказательство

Сначала доказывается, что существование содержащего все ребра замкнутого пути без кратных ребер равносильно четности всех вершин. Если граф эйлеров, то добавим ребро, соединяющее первую и последнюю вершину эйлерового пути. Получим, что все вершины дополненного графа имеют четные степени.

Пример

Рассмотрим графы (рис. 4.2) («открытое письмо» и «закрытое письмо») и проверим, являются ли они эйлеровыми. Поскольку граф (см. рис. 4.2, а)  («закрытое письмо») имеет четыре вершины нечетной степени, то согласно теореме  он не будет эйлеровым. Значит,  его  невозможно  нарисовать, не  отрывая карандаш и проходя каждую линию ровно один раз.

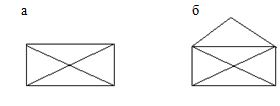
Рис. 4.2. Графы «закрытое письмо» (а) и «открытое письмо» (б)

Второй граф (см. рис. 4.2, б) имеет две вершины нечетной степени, следовательно, согласно теореме  он является эйлеровым, и его можно нарисовать, не отрывая карандаш и проходя каждую линию ровно один раз.