Для решения трех основных задач синтеза уравнения, получаемые инверсией системы уравнений, в обобщенной форме будут иметь следующий вид.
1) Для функционального синтеза
|
![]()
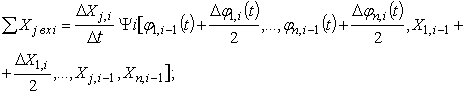
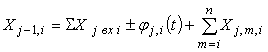
где j = 1, 2, 3, …, n – номер уравнения; i = 1, 2, 3… – номер шага; т =- j,j+1,…,n – номер координаты обратной связи, воздействующей на вход рассматриваемого звена; Σ![]() – суммарное входное воздействие на рассматриваемое звено; φj,i (t) – внешнее возмущающее воздействие на звено; Σ Xj,m,i – суммарное воздействие обратных связей на рассматриваемое звено; Ψi – инверсная функция, определяемая видом правой части уравнений (4.1).
– суммарное входное воздействие на рассматриваемое звено; φj,i (t) – внешнее возмущающее воздействие на звено; Σ Xj,m,i – суммарное воздействие обратных связей на рассматриваемое звено; Ψi – инверсная функция, определяемая видом правой части уравнений (4.1).
Сущность этой наиболее простой части общего синтеза заключается в том, что последовательно для каждого звена по известному или найденному на предыдущем этапе синтеза закону изменения выходной координаты, по инверсному уравнению вида (4.1) определяется суммарное входное воздействие на рассматриваемое звено (функция управления). Затем из последнего вычитаются внешнее воздействие и воздействие обратных связей и определяется закон изменения выходной координаты следующего по ходу синтеза звена.
Следует иметь в виду, что в уравнение (4.1) входят усредненные значения величин на каждом рассматриваемом шаге i. Функция управления на входе системы (первое звено) находится аналогично по формулам (4.1), но зависимость φ1,i (t) в правой части, как правило, отсутствует, поскольку она является искомой и φ1,i (t) = х0,i.
2) Для параметрического синтеза, т. е. для определения параметров некоторого промежуточного звена c индексом j, необходимо определить законы изменения его входного воздействия ΣXj вх и выходной координаты Xj (рис. 4.1).
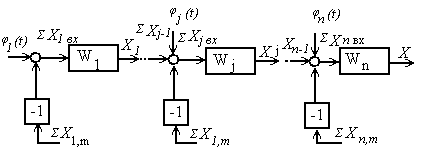 |
Рис. 4.1. Схема синтеза
Эта задача осуществляется ходом «справа» и «слева», т. е. решением системы уравнений вида:
Xk,I = Xk,I-1 + Δt fk [φ1,I-1 (t) + Δ φ 1,I (t) / 2, … ,φ n,I-1 (t) + Δ φ n,I (t), (4.2)
X1,I-1 + ΔX1,I / 2, … , Xk-1,I-1 + ΔXk-1,I / 2 , Xk,I-1, … , Xn,I-1],
где k = 1, 2, 3, …, j – 1;
![]()
![]() (4.3)
(4.3)
где l = j + 1, j + 2, …, п;
![]()
![]() . (4.4)
. (4.4)
Зная структуру звена и законы изменения входного воздействия (4.2) и выходной координаты (4.4), нетрудно определить искомые варьируемые параметры. Если таких варьируемых параметров один, то задача его нахождения решается однозначно. Если варьируемых параметров несколько, то, варьируя значения одних в наиболее благоприятной и желаемой зоне их изменения, определяют искомые значения остальных.
3) Для структурно-параметрического синтеза, т. е. для определения числа, вида и места включения обратных связей, необходимо найти дополнительное входное воздействие на звено, реализация которого осуществляется обратными связями. Для этого по уравнению (4.2) определяется суммарное входное воздействие на синтезируемое звено, которое необходимо для реализации оптимального закона изменения выходной координаты.
Искомое воздействие обратных связей определяется из соотношения
![]()
![]() . (4.5)
. (4.5)
В уравнении (4.5) закон изменения выходной координаты предыдущего звена (прямая связь) Xj-1,i предполагается известным: он может быть либо задан, либо при известной структуре предыдущих звеньев легко определен решением системы уравнений вида (4.3). В противном случае проектировщик определяет желаемый закон изменения выходной координаты Xj-1,i, исходя из соображений наилучшего удовлет- ворения задаче последующих этапов синтеза по нему структуры других звеньев (k = 1, 2, 3, j-1).
Если возникает задача определения структуры и нелинейных характеристик самого звена при отсутствии обратных связей, то она решается на основании уравнений (4.2) – (4.4) нахождением законов изменения входного воздействия и выходной координаты звена и последующим определением по ним искомых нелинейных характеристик. Такая задача, например, возникает при синтезе компенсационных регуляторов в системах идентификации для компенсации инерционности и нелинейностей звеньев основной структуры объекта управления.