Логарифмические амплитудно- и фазо-частотные характеристики (ЛАХ и ФЧХ) широко используются при анализе и синтезе непрерывных САУ. Но для дискретных систем использование обычных методов построения этих характеристик невозможно. Причина в том, что передаточные функции непрерывных САУ, по которым осуществляется построение характеристик, являются дробно-рациональными функциями комплексной переменной p и могут быть выражены в виде линейных или квадратичных множителей, а передаточные функции дискретных систем являются трансцендентными функциями оператора p.

Z-преобразование превращает трансцендентную передаточную функцию от p в рациональную функции от z. Но для построения ЛАХ и ФХЧ необходимо также, чтобы с изменением частоты  комплексная переменная, являющаяся аргументом передаточной функции, изменялась вдоль мнимой оси комплексной плоскости (например ). Но поскольку зависимость между комплексными переменными z и p определяются формулой (2.3), и, следовательно:

то при изменении частоты комплексная переменная z перемещается по единичной окружности вокруг начала координат комплексной плоскости Z.

Поэтому необходимо введение такого преобразования, которое отражало бы единичную окружность на плоскости Z в мнимую ось другой комплексной плоскости. Такое отображение осуществляется с помощью билинейного преобразования (3.1), в соответствии с которым внутренняя часть единичного круга на z-плоскости отображается в левую полуплоскость w, а внешняя часть этого круга – в правую полуплоскость.

Зависимость между w и  имеет вид:

                                        (4.3)

Следовательно, при изменении частоты  комплексная переменная w перемещается вдоль мнимой оси.

Введем в рассмотрение относительную псевдочастоту , равную:

                                                        (4.4)

На основании выражений (4.3) и (4.4) может быть получена зависимость между  и комплексной переменной w:

,

которая аналогична зависимости . Разница лишь в том, что , в отличие от , является безразмерной величиной. Поэтому при построении ЛАХ и ФЧХ дискретных систем будем использовать абсолютную псевдочастоту l, которая как и , измеряется в секундах в минус первой степени ():

.

Зависимость между абсолютной псевдочастотой и переменной w имеет вид:

Таким образом, построение ЛАХ дискретной САУ осуществляется в следующей последовательности: по передаточной функции системы  на основании (3.1) вычисляется передаточная функция , по которой с учетом выражения  (4.6), определяется частотная характеристика .

Построение асимптотической ЛАХ по виду  производится по тем же правилам, что и для непрерывных систем. При построении ФЧХ следует обращать внимание на наличие неминимально-фазового сомножителя  в числителе функции . Определяемая им составляющая в ФЧХ равна:

.

В диапазоне частот, где  выполняется равенство: , и, следовательно, построение ЛАХ и ФЧХ дискретных систем можно производить непосредственно по передаточной функции ПНЧ . Это значительно упрощает анализ точности дискретных САУ, осуществляемый по виду низкочастотного участка ЛАХ.

Пример 23

Необходимо построить ЛАХ и ФЧХ дискретной САУ, передаточная функция которой:

.

Преобразованная передаточная функция:

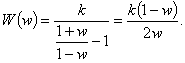
Частотная характеристика имеет вид:

.

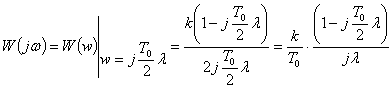Логарифмическая амплитудно-частотная характеристика:

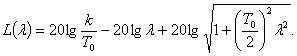
Фазо-частотная характеристика:

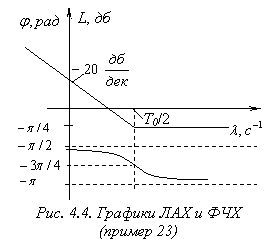
Графики логарифмической амплитудно- частотной и фазо-частотной характеристик приведены на рис. 4.4.