Каждое уравнение в системе нелинейных уравнений в общем случае определяет некоторую поверхность: ![]() . Решениями системы нелинейных уравнений являются точки пересечения этих поверхностей. Таким образом, происходит графическое отделение решений.
. Решениями системы нелинейных уравнений являются точки пересечения этих поверхностей. Таким образом, происходит графическое отделение решений.
Пример
Отделить выпуклую область D, содержащую одно решение системы
![]() ,
,
где х, y измеряются в радианах.
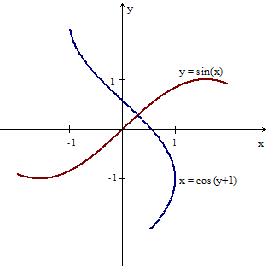
Рис. 4.1. Отделение решения
Решение
Построим графики: ![]() и
и ![]() (рис 4.1) и будем искать их точки пересечения. Уравнения удобно записать в виде:
(рис 4.1) и будем искать их точки пересечения. Уравнения удобно записать в виде:
![]() ,
, ![]() .
.
Область ![]() содержит одно решение системы нелинейных уравнений. D – квадрат, следовательно, D – выпуклая область. Область
содержит одно решение системы нелинейных уравнений. D – квадрат, следовательно, D – выпуклая область. Область ![]() является решением задачи отделения решения системы нелинейных уравнений.
является решением задачи отделения решения системы нелинейных уравнений.
При необходимости D можно уменьшить до области D1:
![]() .
.