Область использования метода динамического программирования не ограничивается динамическими задачами, в которых явно присутствует время. Успех применения метода динамического программирования к решению оптимизационной задачи связан со специальной структурой целевой функции и функций ограничений. Наиболее удобным для использования этого метода являются функции аддитивного (сепарабельного) вида.

Рассмотрим пример применения метода динамического программирования к решению задачи, которую можно интерпретировать как задачу распределения ресурсов между технологическими процессами. Имеется  технологических процессов, по которым надо распределить однородный ресурс (например, деньги, или рабочую силу, или энергию) так, чтобы максимизировать общий доход. Пусть использование в -м технологическом процессе ресурса в количестве  приносит доход , а общее количество ресурса равняется . Тогда задача состоит в максимизации функции:

при ограничении

.

Рассмотрим наряду с этой задачей класс аналогичных задач, в которых может меняться число процессов и общее количество ресурсов. Обозначим оптимальное значение в задаче с  процессами и количеством ресурсов  через , тогда в исходной задаче оптимальное значение равно .

Для поставленных задач справедлив принцип оптимальности, который здесь можно сформулировать следующим образом: если для всех процессов в задаче весь ресурс распределен оптимально, то для части процессов приходящаяся на них при таком распределении доля ресурса также должна быть распределена оптимально. Если этот принцип применить к задаче с  процессами и количеством ресурса  и предположить, что в -й процесс вкладывается количество ресурса , то получим формулу:

              (4.11)

Эта формула справедлива при любых  и , поэтому для исходной задачи имеем цепочку соотношений:

;

и т.д.

Для первого процесса, когда ресурсы по остальным процессам уже распределены, получим:

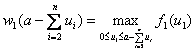.                   (4.12)

С помощью таких рекуррентных соотношений можно решить задачу оптимального распределения ресурсов. Для иллюстрации этой вычислительной процедуры рассмотрим конкретный пример с .

Итак, требуется максимизировать функцию:

при ограничении

.

Согласно формуле (4.12) имеем:

,

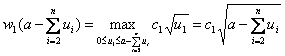а условно оптимальное использование ресурса в первом процессе есть

.

Далее для двух технологических процессов находим оптимальное распределение ресурсов:

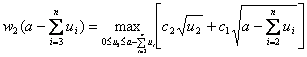.               (4.13)

Дифференцируя выражение в квадратных скобках в формуле (4.13) по , и приравнивая производную к нулю, получим соотношение:

,

откуда 

;           .

Используя вторую производную, легко убедиться, что  дает именно максимум выражению в квадратных скобках в формуле (4.13).

На следующем шаге распределяем ресурсы для трех технологических процессов:

.

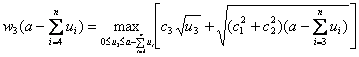Решая задачу максимизации, как и на предыдущем шаге, получим:

;

.

Продолжая вычисления по процедуре, получим общие выражения для  и :

;

.

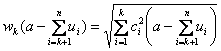Так как для последнего технологического процесса должно выполняться ограничение , то на -м шаге находим просто оптимальное значение задачи

и оптимальное использование ресурса в -м процессе

.

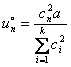Подставляя  в выражение для , затем в выражение для  и т.д., получим решение задачи:

.

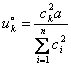Конечно, в рассмотренном примере решение может быть получено (и притом более просто) за один шаг с использованием метода Лагранжа, но в более сложных задачах подобного типа метод динамического программирования может оказаться самым эффективным.