Атрибутные МП-автоматы отличаются от обыкновенных МП-автоматов тем, что символы и состояния снабжены атрибутами, которые обрабатываются в процессе его работы. Атрибутный МП-автомат обладает следующими свойствами:

1) Все входные, выходные и магазинные символы, а также состояния имеют конечное число атрибутов.

2) На каждом шаге работы атрибутного МП-автомата значения атри­бутов нового состояния, нового верхнего символа магазина (если этот шаг не выталкивание из магазина) и выходных символов вычисляют­ся как функция атрибутов старого состояния, верхнего символа мага­зина и входного символа (если это не пустой шаг).

Определение 4.3.3. [17]. Атрибутный МП-преобразователь – это система из 11 объектов:

M = <Q, I, Y, Г, , q, Z, A, C, u, v>,

где       Q         – конечное множество состояний;

  I           – конечное множество входных символов;

  Y         – конечное множество выходных символов;

  Г          – конечное множество магазинных символов;

  qQ    – начальное состояние;

  ZГ    – начальный магазинный символ;

  A         – множество возможных значений атрибутов;

  С         – функция из QIYГ во множество неотрицательных целых чисел, определяющая, сколько атрибутов имеет каждый символ; посредством будет обозначаться расширение С на множество { QIYГ}*, получаемое, если положить () =  и () = С()+С(), где – пустой символ, – символ, – цепочка символов;

uA^C(q) – множество значений атрибутов для начального состояния;

v A^C(q) – множество значений атрибутов для начального магазинного символа;

 – отображение {Qx            {I{}}xГ} во множестве конечных множеств четверок, такое, что если (r, , ) содержит (p, , , f), то pQ, Г*, Y* и f – вычислимая функция, кроме того всякие две четверки в (r, , ) отличаются по крайне мере одной из трех своих компонент.

Атрибутный МП-преобразователь называют детерминированным, если:

1) для любых rQ и Г всякий раз, когда (r, , ) не пусто, (r,,) пусто для всех ;

2)  отображает аргумент во множество, состоящее не более чем из одного элемента.

Конфигурация атрибутного МП-преобразователя — это четверка (r, х, , у), где   r — атрибутное состояние, х — цепочка атрибутных входных символов,  — цепочка атрибутных магазинных символов, у — цепочка атрибутных выходных символов. Если конфигурация имеет вид (r_g, _h, x, , , y), где r — состояние со множе­ством атрибутов g, I {} имеет множество атрибутов h,  — магазинный символ со множеством атрибутов i, и (r, , )  содержит (р, n, , f), то мы пишем:

(r_g, _h, x, , , y)  (, x, ,, y),

где , , – это p, ,, соответственно с атрибутами, вычисленными в результате применения функции f к атрибутам из g, h, i.

Рефлексивное транзитивное замыкание отношения  обозначается как *

Если

(q_u, x, Z_v,) ^*(p, ,, y),

т.е. цепочку называют трансляцией цепочки х, выполняемой атрибутным МП-преобразователем.

Теорема 4.3.1. [17]. Любую трансляцию, определяемую L-атрибутной транс­ляционной грамматикой, у которой входная грамматика является LL(1)-грамматикой, можно выполнить на атрибутной детерминированной МП-машине с концевым маркером.

Доказательство данной теоремы [17] является, no-существу, описанием ал­горитма построения атрибутного МП-преобразователя по трансляционной LL(K)-грамматике. Воспроизведем основные шаги этого алгоритма.

Пусть I — входное множество трансляционной грамматики, Y — множество операционных символов (символов действий), N — множество нетерминалов. Перенумеруем правила грамматики числами от 1 до га, где m — число правил в грамматике. Пусть в правой части i-го правила содержится n_i символов.

Атрибутный МП-преобразователь имеет вид

M = <{q}, I, Y, {z}{(i, j) | 1im, 0jn}, , q, Z, A, C, u, v>,

где q, Z – произвольные новые имена, А – множество значений атрибутов грамматики, u – произвольно, C, v,  определяют ниже.

Для IY значение С() равно числу атрибутов, которыми обладает  в грамматике. Для Z C(Z) = , для q C(q) = max C(), где . Для каждого магазинного символа вида (i, j) значение C((i, j)) равно сумме числа атрибутов первых j = 1 символов правой части i-го правила и числа унаследо­ванных атрибутов нетерминала, стоящего в левой части правила.

Атрибутный МП-автомат выполняет нисходящий разбор. Когда магазинный символ (i, j) находится наверху магазина, значения унаследованных атрибутов левой части 1-го правила и всех атрибутов первых j символов правой части известны — они равны значениям соответствующих атрибутов состояния (для j-ro символа правой части) и верхнего символа магазина (для первых j = 1 сим­волов его правой части).

Магазинный символ Z используется только лишь для инициализации рабо­ты магазина и после первого же такта работы автомата выталкивается из мага­зина. Символ Z в первом такте заменяется на (i, 0)—это означает, что начальный символ грамматики разворачивается по i-му правилу. При этом символ (i, 0) имеет столько атрибутов, сколько имеется унаследованных атрибутов у началь­ного символа грамматики, а их значения полагаются равными значениям, кото­рые заданы для унаследованных атрибутов в грамматике.

Когда верхний символ магазина имеет вид (i, j), где j = n_i, это означает, что i-е правило применилось успешно.

Очередное действие автомата — подмножеству атрибутов состояния присва­иваются значения атрибутов левой части правила, а верхний символ выталкива­ется из магазина. При этом значения унаследованных атрибутов равны значениям соответствующих атрибутов символа (i, j). Значения синтезированных атрибу­тов вычисляются по значениям атрибутов символа (i, j) и состояния q.

Действия МП-автомата, когда верхним символом магазина является символ (i, j), где j<n, зависят от того, является ли (j+1) символ правой части правила входным, нетерминальным или операционным. Во всех этих слу­чаях символ (i, j) будет замещен символом (i, j+1), а значения атрибутов этого символа будут вычисляться по значениям атрибутов символа (i, j) и состояния q. Действия же автомата для различных типов символа (i, j+1) будут различны. Обозначим (j+1)-й символ 1-го правила через а и рассмот­рим основные случаи.

Случай 1.  , т.е. а — входной символ. Если  совпадает с текущим вход­ным символом, то атрибутам состояния q присваиваются значения атрибутов символа .

Случай 2.  Y, т.е. — операционный символ. Унаследованные атрибуты для вычисляются по значениям атрибутов символа (i, j) и состояния q. Син­тезированные атрибуты вычисляются после нахождения значений унаследо­ванных. После этого символ  вместе со значениями его атрибутов выводится на выходную ленту МП-преобразователя.

Случай 3. , т.е.  — нетерминальный символ. МП-преобразователь выби­рает k-e правило, левой частью которого является а, и помещает на верх магазина (над символом (i, j+1)) символ (k, 0), присваивая его атрибутам значения унаследо­ванных атрибутов символа. Впоследствии, когда символ (i, j+1) вновь станет верх­ним символом магазина (после выталкивания символа (k, n_k)), значения атрибутов символа  будут равны значениям некоторых атрибутов состояния.

Пример 4.3.2. Процесс построения атрибутного МП-преобразователя рас­смотрим на примере трансляции оператора описания переменных в некотором гипотетическом языке программирования. Будем полагать, что описание пере­менных задается, например, в виде:

real i₁, i₄, i₉.

Здесь символ i_k является идентификатором, индекс k является атрибутом, причем значением этого атрибута служит указатель на позицию таблицы иден­тификаторов, сопоставленную данному идентификатору. Для каждого иденти­фикатора во время трансляции необходимо выполнить операцию ALLOCATE. В результате выполнения этой операции в позицию таблицы идентификато­ров, соответствующую данному, заносится адрес ячейки памяти, выделяемой этому идентификатору. Будем считать, что для идентификатора выделяется одна ячейка памяти. Выделяются ячейки последовательно, начиная с ячейки с адре­сом 50. Операция ALLOCATE реализуется одноименной семантической про­граммой, которая имеет два входных параметра: указатель на соответствующую позицию таблицы идентификаторов, а также адрес выделенной для идентифи­катора ячейки памяти.

Описанный содержательно процесс трансляции (семантика) оператора описания переменных может быть формально задан с помощью L-атрибутной трансляционной грамматики, приведенной на рис. 4.11 [17].

Нижние символы возле символов грамматики — имена атрибутов, верх­ние — имена магазинных символов для МП-преобразователя, задаваемые в виде пары (i, j), где i — номер правила, j — позиция символа в правиле. Для входной цепочки real i₁, i₄, i₉, данная грамматика порождает следующую актив­ную цепочку:

real i₁, {ALLOCATE}_{1, 50}, i₄ { ALLOCATE}_{4, 51}, i₉ {ALLOCATE}_9,52

Для построения атрибутного МП-преобразователя, выполняющего такие трансляции, будем использовать результаты теоремы [17].

Y = {{ALLOCATE}_a2,x2} – множество операционных символов;

S_{x1, z2} – наследуемый х1, синтезируемый z2

R_{x1, x2} – наследуемый х1, синтезируемый х2

{ALLOCATE}_a2,x2 – наследуемые а2, х2

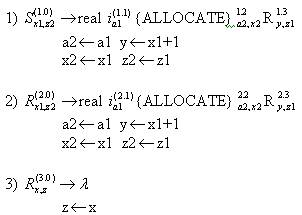
Рис. 4.11. L-атрибутная трансляционная грамматика для оператора описания переменных

Имеем:

{q} = {q, ДОПУСТИТЬ, ОТВЕРГНУТЬ} – множество состояний МП-преобразователя;

I = {real, i_a1, ,} – множество входных символов;

Г = {#, (1,0), (1,1), (1,2), (1,3), (2,0), (2,1), (2,2), (3,0)) – множество магазинных символов. Отображение зададим в виде равенств вида

(q, x, y) = (q,           , ),

где х – входной символ, у – магазинный символ, – новый магазинный символ (или цепочка символов), – выходной символ. Если x = , то это означает — любой входной символ без сдвига входной ленты, если =, то выполняется только выталкивание символа из магазина, если = , — на выходную ленту ничего не записывается. Имеем:

(q, real, (1, 0)) = (q, (1, 3), (1, 2), (1, 1), );

(q, i, (1, 1)) = (q, , );

(q, , (1, 2)) = (q, , (1, 2));

(q, , , (1, 3)) = (q, (2,0), );

(q, , (2, 0)) = (q, (2, 3), (2, 2), (2, 1), );

(q, i, (2, 1)) = (q, , );

(q, , (2, 2)) = (q, , (2, 2));

(q, , , (2, 3)) = (q, (2,0), );

(q, , (2, 3)) = (q, (3,0), );

(q, , (1, 3)) = (q, (3,0), );

(q, , (3, 0)) = (q, , );

(q, , #) = (ДОПУСТИТЬ, , );

Во всех других ситуациях автомат переходит в состояние ОТВЕРГНУТЬ.

Последовательность конфигураций МП-преобразователя при выполнении трансляции входной цепочки real i₁, i₄ – будет следующей:

(q_0,0,0, real i₁, i₄ , #(1,0)_50,0,)

(q_50,0,0,       i₁, i₄ , #(1,3)_0,0 (1,2)_0,0 (1,1)₀,)

(q_50,1,0,         , i₄ , #(1,3)_51,0 (1,2)_1,50)

(q_50,1,51,          i₄ , #(2,0)_51,0 (1,2)_1,50)

(q_50,1,51,             , #(2,3)_0,0 (2,2)_0,0 (2,1)_0,0 (1,2)_1,50)

(q_50,4,51,             , #(2,3)_52,0 (2,2)_4,51 (1,2)_1,50)

(q_50,4,51,             , #(3,0)_52,52 (1,2)_1,50 (2,2)_4,51)

(q_50,4,51,             , #(1,2)_1,50 (2,2)_4,51)

(ДОПУСТИТЬ,, #(1,2)_1,50 (2,2)_4,51)

Таким образом, на выходной ленте атрибутного МП-преобразователя будет сформирована следующая операционная часть активной цепочки:

{ALLOCATE}_1,50, {ALLOCATE}_4,51.