Опосредованные умозаключения – это те, в которых вывод делается из двух и более посылок.
Существует несколько видов опосредованных умозаключений. К ним относятся:
1) опосредованные умозаключения из простых атрибутивных суждений;
2) опосредованные умозаключения из суждений об отношениях;
3) опосредованные умозаключения из сложных суждений.
Опосредованные умозаключения из простых атрибутивных суждений. Наиболее распространённой и важной их формой является простой категорический силлогизм (от греч. syllogismos – сосчитывание, выведение следствия). Он называется простым, потому что состоит всего из двух посылок и заключения. Эти посылки и заключение состоят из терминов. Их три: меньший, больший и средний. Меньшим термином называется субъект заключения, а большим термином – предикат заключения. Они обозначаются соответственно буквами «S» и «P». Средний термин не входит в заключение, но входит в обе посылки, обеспечивая логическую связь между ними. Он обозначается буквой «M» (от лат. terminus medius – термин средний).
Посылка, в которую входит больший термин, называется большей, а посылка, в которую входит меньший термин, – меньшей.
Рассмотрим структуру простого категорического силлогизма на примере:
Все киты (M) – млекопитающие (P). (Большая посылка)
Все кашалоты (S) – киты (M). (Меньшая посылка)
Все кашалоты (S) – млекопитающие (P). (Заключение)
Черта, отделяющая посылки от заключения, означает слово «следовательно».
В логике сформулированы общие правила простого категорического силлогизма, которые нужно выполнять, чтобы при истинных посылках заключение было истинным. Таких правил семь:
1) по крайней мере, одна из посылок должна быть общим суждением;
2) по крайней мере, одна из посылок должна быть утвердительной;
3) при одной частной посылке заключение должно быть частным;
4) при одной отрицательной посылке заключение должно быть отрицательным;
5) при обеих утвердительных посылках заключение должно быть утвердительным;
6) средний термин должен быть распределен, по крайней мере, в одной из посылок;
7) термин, не распределённый в посылке, не должен быть распределённым в заключении.
Простой категорический силлогизм имеет свои формы, которые называются фигурами силлогизма. Они различаются по положению терминов в его посылках. Этих фигур четыре. Схематически фигуры изображаются так:
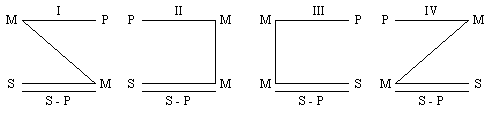
Приведённый ранее силлогизм построен по 1-й фигуре.
Каждая фигура категорического силлогизма имеет свои разновидности, которые называются модусами. Они различаются качественной и количественной характеристикой входящих в них посылок и заключения. Посылки и заключение, таким образом, в каждом случае могут выступать как суждения того или иного вида (A, E, I, O). На первом месте в
символическом выражении модуса записывается большая посылка, на втором – меньшая, на третьем – заключение. Так, выражение для модуса AAA означает, что большая и меньшая посылки, а также заключение в нём являются общеутвердительными суждениями. Эту форму модуса имеет, кстати говоря, ранее приведённый силлогизм о кашалотах.
Общее число модусов силлогизма – 256 (по 64 в каждой фигуре). Из них правильными (т. е. такими, которые при истинности посылок всегда дают истинное заключение) могут быть 24, включая и так называемые ослабленные модусы, т.е. такие, для которых существуют модусы, дающие более сильные заключения. Модус называется более слабым, если мы получаем в заключении суждения вида I и O, хотя можем получить соответственно суждения A и E. Неослабленных модусов фигур силлогизма – 19.
Модусы 1-й фигуры: AAA, EAE, AII, EIO.
Модусы 2-й фигуры: AEE, AOO, EAE, EIO.
Модусы 3-й фигуры: AAI, EAO, IAI, OAO, AII, EIO.
Модусы 4-й фигуры: AAI, AEE, IAI, EAO, EIO.
Кроме общих правил категорического силлогизма, существуют специальные правила фигур силлогизма. Каждая из фигур имеет особые правила, вытекающие из общих. Приведём правила трёх первых фигур.
Правила 1-й фигуры:
1) большая посылка должна быть общим суждением (общеутвердительным или общеотрицательным);
2) меньшая посылка должна быть утвердительным суждением (общеутвердительным или частноутвердительным).
Правила 2-й фигуры:
1) большая посылка должна быть общим суждением;
2) одна из посылок должна быть отрицательным суждением.
Правила 3-й фигуры:
1) меньшая посылка должна быть утвердительным суждением;
2) заключение должно быть частным суждением.
Простой категорический силлогизм может быть полным и сокращённым. Сокращённый категорический силлогизм называется энтимемой (от греч. in thymos – в уме). В таком силлогизме пропущена одна из посылок или заключение. Примером энтимемы является такое умозаключение: «Все кашалоты – киты, следовательно, все кашалоты – млекопитающие». В этом умозаключении пропущена большая посылка: «Все киты – млекопитающие». Ещё пример: «Все металлы – теплопроводны, следовательно, и алюминий теплопроводен». Здесь пропущена меньшая посылка: «Алюминий – металл».
Нужно иметь в виду, что энтимемами пользуются чаще, чем полными категорическими силлогизмами. Обоснованием для опускания посылок или заключения в силлогических умозаключениях, осуществляемых в ходе каких-либо рассуждений, является якобы простота подразумевания пропущенных элементов. Однако иногда энтимемы могут быть неправильно составленными. Для проверки энтимем на истинность в логике разработаны правила восстановления их в полные силлогизмы. Так, если обнаружится, что нарушено хотя бы одно правило силлогизма, то энтимема будет признана ошибочной.
В процессе мышления имеют место не только простые силлогизмы, но и сложные, состоящие из двух, трёх или большего числа простых силлогизмов. Такие цепи силлогизмов называются полисиллогизмами (от греч. poly – много). Например:
Все растения – живые организмы.
Все цветы – растения.
Все цветы – живые организмы.
Заключение этого полного простого силлогизма может быть, в свою очередь, использовано в качестве большой посылки нового полного простого силлогизма:
Все цветы – живые организмы.
Роза – цветок.
Роза – живой организм.
В итоге получается полисиллогизм.
Нетрудно заметить, что первое, т.е. промежуточное, заключение может быть опущено. И тогда всё умозаключение в целом примет следующий вид:
Все растения – живые организмы.
Все цветы – растения.
Роза – цветок.
Роза – живой организм.
Такой полисиллогизм, в котором пропущено, по крайней мере, одно промежуточное заключение, называется соритом (от греч. soros – куча). Сориты в рассуждениях применяются чаще, чем полисиллогизмы, так как являются сокращённой формой полисиллогизмов.
Существует ещё один вид полисиллогизма, в котором обе посылки представляют собой энтимемы. Такой полисиллогизм называется эпихейремой (от греч. epiheirema – умозаключение). Приведём пример:
Ложь заслуживает презрения, так как она безнравственна.
Лесть есть ложь, так как она есть умышленное извращение истины.
Лесть заслуживает презрения.
Опосредованные умозаключения из суждений с отношениями значительно отличаются от умозаключений из простых атрибутивных суждений. Это видно на следующем примере:
Неапольский университет основан раньше Пражского.
Пражский университет основан раньше Краковского.
Неапольский университет основан раньше Краковского.
Символически:
xRy
yRz
Rtrans
xRz
Опосредованные умозаключения из сложных суждений также имеют свою специфику. Логическое следование заключения из посылок определяется в них не субъектно-предикатными отношениями, как в умозаключениях из простых суждений, а лишь логической связью между составляющими сложного суждения.
В зависимости от характера этой связи выделяются следующие виды опосредованных умозаключений из сложных суждений:
1) условно-категорические;
2) разделительно-категорические;
3) условно-разделительные.
Условно-категорические умозаключения состоят из двух посылок, одна из которых – импликативное суждение. Другая посылка и заключение могут быть либо антецедентом, либо консеквентом первой посылки, либо отрицанием того или другого. К числу правильных условно-категорических умозаключений относятся:
- modus ponens (утверждающий способ). В символической записи:
A![]() B
B
A
B
Например: Если идёт дождь, то крыши мокрые.
Дождь идёт.
Крыши мокрые.
- modus tollens (отрицающий способ). Символически:
A![]() B
B
![]() B
B
![]() A
A
Например: Если наступает осень, то с деревьев опадают листья.
Листья с деревьев не опадают.
Осень не наступила.
Разделительно-категорические умозаключения также состоят из двух посылок. Одна из посылок является дизъюнктивным или строго дизъюнктивным суждением. Другая же посылка и заключение совпадают с одним из составляющих дизъюнктивного или строго дизъюнктивного суждения или с его отрицанием. К числу правильных разделительно-категорических умозаключений относятся:
- modus tollendo-ponens (отрицающе-утверждающий способ). Символически:
A![]() B
B
![]() A
A
B
Например: В автомобиле закончился бензин или он сломался.
Автомобиль не сломался.
В автомобиле закончился бензин.
- modus ponendo tollens (утверждающе-отрицающий способ). Символически:
A![]() B
B
A
![]() B
B
Например:
Организмы бывают либо одноклеточными, либо многоклеточными.
Данный организм является одноклеточным.
Данный организм не является многоклеточным.
Условно-разделительные умозаключения включают несколько импликативных посылок и одну дизъюнктивную посылку. В дизъюнктивной посылке выделяются варианты положения дел. В результате сравнения этих вариантов делается общий вывод. Если число вариантов равно двум, то такие умозаключения называются дилеммами, а если – больше двух, то – полилеммами.
Разновидности дилеммы:
- простая конструктивная дилемма. В символической записи:
A![]() C, B
C, B![]() C
C
A![]() B
B
C
Примером здесь может служить рассуждение Сократа:
Если смерть – переход в небытие, то она благо.
Если смерть – переход в иной мир, то она благо.
Смерть – переход в небытие или мир иной.
Смерть – благо.
- простая деструктивная дилемма. Символически:
A![]() B, A
B, A![]() C
C
![]() B
B![]() C
C
![]() A
A
Например:
Если у меня будет достаточно свободного времени, то я пойду в театр.
Если у меня будет достаточно свободного времени, то я буду оформлять альбом.
Я не пошёл в театр или не оформлял альбом.
У меня не было достаточно свободного времени.
- сложная конструктивная дилемма. Символически:
A![]() C, B
C, B![]() D
D
A![]() B
B
C![]() D
D
Например:
Если пойдёшь направо, то коня потеряешь.
Если пойдёшь налево, то голову потеряешь.
Но нужно идти направо или налево.
Придётся потерять коня или голову.
- сложная деструктивная дилемма. Символически:
A![]() C, B
C, B![]() D
D
![]() C
C![]() D
D
![]() A
A![]() B
B
Например:
Если бы я был богат, то я купил бы себе автомобиль.
Если бы я был министром, то мне предоставили бы казённый автомобиль.
Но у меня нет личного или казённого автомобиля.
Я не богат или я не министр.