Экстремальные эксперименты – это эксперименты, с помощью  которых определяют экстремальные точки, т.е. точки, в которых целевая функция достигает экстремума(max,min) для одно- или многофакторных зависимостей или математических моделей. Такие эксперименты становятся необходимыми в том случае, когда математическое описание объекта или явления отсутствует и оптимизация аналитическим или численным методом невозможна.

Задачу оптимизации в этом случае можно решить экспериментально  двумя способами. Первый из них  – традиционный  – предполагает постановку  обычных  пассивных экспериментов. При использовании второго способа выполняются активные эксперименты с одновременным варьированием  всех влияющих факторов.

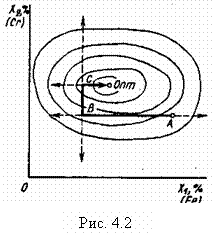
Рассмотрим поиск экстремума пассивным способом на примере двухфакторной зависимости y = f (x₁, x₂) при  неполном знании механизма этой зависимости, где Y – прочность металлического сплава, а   x₁  и  x₂ – содержание железа  и содержание хрома соответственно в данном сплаве в процентах. Покажем поиск оптимума (максимальной прочности сплава) графически. На рис. 4.2 с помощью линий уровня изображена поверхность отклика в двухфакторном пространстве. Точке О_пт  соответствует максимальная прочность сплава.

Начиная эксперименты традиционным способом, берут исходный сплав (рис. 4.2, точка А), содержание хрома сохраняют на постоянном уровне, а содержание железа варьируют. Увеличивая содержание железа (двигаясь вправо вдоль линии абсцисс), довольно быстро устанавливают, что прочность сплава не меняется (направление этого движения бесперспективно). При уменьшении содержания железа (при движении влево вдоль линии абсцисс) прочность сплава сначала увеличивается, а затем уменьшается.

Максимальная прочность сплава (рис. 4.2) соответствует точке В. Теперь содержание железа сохраняют на постоянном уровне, а изменяют содержание хрома. Из точки В проверяют два направления движения (вниз и вверх от оси ординат). При увеличении содержания хрома (движении вверх по оси ординат) находят новую перспективную точку С, от которой снова, переходя к варьированию содержания железа, приходят в оптимум – точку О_пт.

Рис. 4.2 дает представление о следующих особенностях пассивных экспериментов:

1) штриховые линии отображают эксперимент, проведенный впустую (ошибочные направления движения к оптимуму);

2) поиск оптимума ведется фактически вслепую методом попыток;

3) сплошная линия, представляющая собой правильное направление движения к оптимуму, не является кратчайшим расстоянием от точки А до точки О_пт;

4) при увеличении числа факторов  X_J  процедура поиска оптимума резко усложняется.

При постановке активных экспериментов по методу градиента в окрестностях исходной точки А поверхность отклика аппроксимируют плоскостью, на которой ставят 2^К опытов по плану ПФЭ. По результатам эксперимента строят линейный  полином вида:

y = b_O + b₁x₁ + b₂x₂.

Затем по найденному уравнению полинома отыскивают положительный градиент функции у, то есть направление дальнейшего движения по поверхности отклика, которое приводит к наискорейшему увеличению функции y (самый «крутой склон»). Движение по «крутому склону» продолжают до точки О_пт  с промежуточными проверками направления движения по градиенту. Метод градиента является наиболее эффективным по сравнению с другими методами. Его основное преимущество – кратчайший путь движения от точки А до точки О_пт  при минимальном количестве опытов при любом количестве влияющих факторов.

Другие методы поиска оптимума (симплексный метод, метод случайного поиска также) могут быть применены для проведения экстремальных поисковых экспериментов /3, 4/. Более подробно метод градиента описан в следующем подразделе.