Пусть известна выпуклая область D, содержащая одно решение системы нелинейных уравнений:

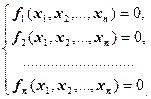            или в векторном виде:      .

Пусть функции  являются дважды непрерывно дифференцируемыми в  D  (),  и определитель матрицы Якоби не равен нулю в области D:

,          в  D.

Тогда можно построить последовательность , каждый элемент которой является вектором размерности n:  , и которая определяется по формуле:

,   где  .

Неудобство этой формулы заключается в необходимости вычисления обратной матрицы. Из теории систем линейных уравнений мы помним, что, с точки зрения вычислительной математики, решение систем линейных уравнений проще и устойчивее, чем обращение матрицы. Так как , то умножим обе части на  и получим:

   или   .

То есть мы получили систему линейных уравнений: , где ,    , . Здесь  – неизвестный вектор,  – известный вектор.

Условие сходимости метода Ньютона сформулируем нестрого.

Если вектор начального приближения   выбран достаточно близко к точному решению, то последовательность , построенная методом Ньютона, сходится к точному решению системы нелинейных уравнений.

Условие остановки итерационного процесса:

.

Из этого условия вытекает, что , где с – точное решение системы нелинейных уравнений; p – положительная константа, не зависящая от e.

Пример

Построить алгоритм решения системы нелинейных уравнений методом Ньютона с точностью :

Решение

1. В примере (разд. 4.2) мы отделили выпуклую область: , содержащую одно решение системы нелинейных уравнений. В нашем случае:

Функции  дважды непрерывно дифференцируемы в области D. Построим матрицу Якоби:

,               ,

,       ,                 .

Найдём определитель матрицы Якоби (якобиан) и докажем, что он не равен нулю в области D:

.

Докажем, что выражение  не принимает значение  -1 в области D:

при ,      ,

при ,       , следовательно,     , .

2. При выполнении этих условий можно применять метод Ньютона:

.

Запишем формулу метода Ньютона в развёрнутом виде:

.

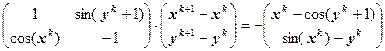Мы получили систему линейных уравнений. Эта система линейных уравнений решается методом Гаусса с частичным выбором ведущего элемента.

3. Выбираем точку начального приближения:   .

4. Условие остановки итерационного процесса:

.

Для первой нормы вектора условие остановки итерационного процесса запишется в виде:

.

Вектор , для которого выполняется условие остановки итерационного процесса, является приближенным решением, полученным методом Ньютона.

Недостатки метода Ньютона

1. Для применения метода Ньютона необходимо близкое к точному решению начальное приближение. Если начальное приближение задано грубо, то метод может разойтись или привести к другому решению.

2. На каждом шаге k итерационного процесса необходимо решать систему линейных уравнений или находить обратную матрицу, а это требует O() арифметических действий для каждого k.