Некоторые задачи динамического программирования могут быть представлены в сетевой постановке. Поэтому вопрос построения сетевых моделей вполне походит для его рассмотрения в этом разделе.
При организации работы над различными проектами, планировании комплексов работ широкое распространение получили методы сетевого планирования и управления. Начальная информация о проекте задается перечнем работ, их продолжительностью или стоимостью, последовательностью выполнения (для каждой работы должно быть указано, каким работам она предшествует или на какую опирается).
Графом называется совокупность множества вершин или узлов и множества дуг или ребер. Каждая дуга задается парой вершин. Сетью называется граф, каждой дуге которого поставлено в соответствие некоторое неотрицательное число. Сетевым графиком проекта называют наглядное представление проекта в виде сети. Дуги этой сети являются ориентированными, т.е. для каждой указаны начало и конец, и представляют работы; вершины (их называют событиями) представляют последовательность выполнения работ. Ни одна работа, представленная дугой, выходящей из некоторой вершины, не может начинаться прежде завершения всех работ, представленных дугами, входящими в данную вершину.
Каждую пару событий должна соединять не более чем одна работа. В сетевом графике должно быть одно начальное и одно конечное событие. Для выполнения перечисленных требований допустимо введение фиктивных работ (работ нулевой продолжительности, не требующих затраты каких-либо ресурсов).
Обозначим начальное событие 
. Чтобы пронумеровать остальные события нужно для каждого события найти величину, равную максимальному числу дуг в путях, соединяющих с данным событием. События нумеруются по возрастанию этой величины. Если для некоторого числа событий указанная величина одинакова, то эти события нумеруются в произвольном порядке.
Пример
Перечень работ по организации зала на промышленной выставке для демонстрации образцов продукции, выпускаемой производственным объединением, приведен в табл.4.1. Построить сетевой график выполнения комплекса работ.
Решение
Приступая к построению сетевого графика (рис.4.1), замечаем, что работа 1 не опирается ни на какую работу, поэтому она изобразится дугой, выходящей из события 
, означающее исходный момент, с которого начинается выполнение рассматриваемого комплекса работ.
На работу 1 опираются работы 2, 3, 4, поэтому дуги, соответствующие этим работам на сетевом графике будут следовать непосредственно за дугой 1, от события 
, означающего момент окончания работы 1 и начало работ 2, 3, 4.
Таблица 4.1 Работы по организации зала для демонстрации образцов продукции
|
Исходная работа |
Содержание работы |
Опирается на работу |
Продолжительность работы |
|
1 |
Отбор образцов продукции для выставки |
5 |
|
|
2 |
Изготовление информационных и рекламных материалов, указателей, надписей и т.д. |
1 |
10 |
|
3 |
Изготовление стендов и другого оборудования для установки образцов в демонстрационный зал |
1 |
7 |
|
4 |
Доставка образцов в выставочный павильон |
1 |
2 |
|
5 |
Доставка в демонстрационный зал стендов и другого оборудования |
4 |
2 |
|
6 |
Монтаж стендов и другого оборудования |
5 |
3 |
|
7 |
Установка образцов продукции на стендах |
3, 6 |
4 |
|
8 |
Оформление зала и стендов указателями, надписями, рекламными и информационными материалами |
7, 2 |
5 |
|
9 |
Репетиция открытия выставки |
8 |
3 |
На работу 4 опирается работа 5, а на нее – работа 6, что и отражено на сетевом графике следующими друг за другом дугами 5 и 6.
Работа 7 опирается на работы 3 и 6, поэтому дуга 7 исходит из события 
, означающего момент, к которому завершены обе эти работы. Аналогичная ситуация имеет место и для работы 8, исходящей из события 
, означающего факт выполнения работ 2 и 7.
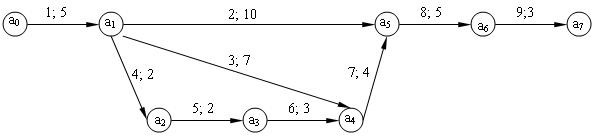
Рис. 4.1. Сетевой график работ
Дуга 9 соответствует последней работе, а конечное ее событие 
означает момент завершения работ всего рассматриваемого комплекса.
На рис. 4.1 рядом с номером работы стоит ее продолжительность в днях.