Основными особенностями трения при резании являются:
· различное физико-механическое состояние контактирующих поверхностей;
· интенсивное схватывание обрабатываемого и инструментального материалов;
· сложный характер распределения нормальных напряжений на контактных площадках;
· малая продолжительность контакта инструмента со стружкой и деталью при постоянном обновлении зоны контакта.
Поверхность трения на передней поверхности инструмента шириной С (рис. 4.6) состоит из двух участков: участка пластического контакта I шириной С1 и участка упругого контакта II.
На участке I расположен заторможенный слой, в пределах которого стружка движется не по передней поверхности, а по заторможенному слою, и сопротивление, оказываемое движению стружки, определяется сопротивлением сдвигу в контактном слое стружки. На этом участке внешнее трение скольжения отсутствует и заменяется «внутренним» трением между отдельными слоями стружки.
На участке II стружка контактирует непосредственно с передней поверхностью. Здесь осуществляется внешнее трение скольжения и сопротивление движению стружки определяется силой трения между стружкой н передней поверхностью. Ширина пластического контакта (C1) зависит от переднего угла инструмента, толщины срезаемого слоя и коэффициента усадки стружки. Н.Г. Абуладзе предложена формула определения ширины пластического контакта
С1 = а [КL (1 – tgg) + secg], (4.1)
где КL – коэффициент усадки стружки.
Из формулы 4.1 видно, что С1 растет при увеличении КL и а, и уменьшается при увеличении угла g. Если инструмент имеет угол наклона лезвия, то при увеличении угла l ширина пластического контакта уменьшается. Отношение С1/С не превышает 0,7 и для обычных конструкционных материалов чаще всего составляет 0,5.
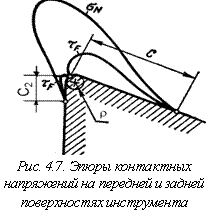
На рисунке 4.7 приведены эпюры контактных напряжений: нормальных (dN) и касательных (tF) на передней и задней поверхностях инструмента, полученные поляризационно-оптическим методом при различных отношениях толщины срезаемого слоя к радиусу округления клина (r).
Эпюра нормальных напряжений непрерывна для площадок контакта С и С2 передней и задней поверхностей, а эпюры касательных напряжений на этих площадках самостоятельны.
Сложный характер контакта на передней поверхности сказывается на распределении контактных напряжений. В настоящее время известно три случая такого распределения на основе расчетно-экспериментальных исследований (рис. 4.8), описанных Н.Н. Зоревым, М.Б. Гордоном и В.Ф. Бобровым.
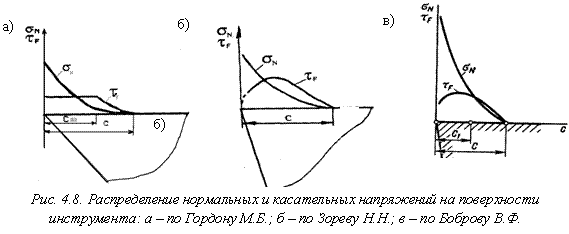
Согласно фундаментальной работе Зорева Н.Н, вблизи режущего лезвия существует пластический контакт, т.е. формируется зона вторичной деформации срезаемого слоя. Протяженность зоны пластического контакта (Спл) составляет 0,4…0,5 от общей длины контакта и существенно определяется скоростью резания (V), толщиной среза (а) и передним углом (g). Максимум коэффициента трения наблюдается при температуре резания 
. При резании большинства металлов коэффициент трения изменяется от 0,5 до 1.
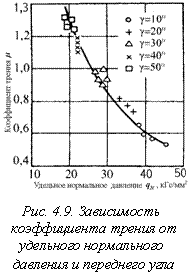
Зорев Н.Н. установил, что зависимость (рис. 4.9) среднего коэффициента трения (m) от условий резания определяется удельными нормальными давлениями (qN) на рабочих поверхностях инструмента. Удельная сила трения (qF) инвариантна к условиям резания, температуре и характеризуется в основном свойствами обрабатываемого материала. В связи с изложенным, средний коэффициент трения определяется по формуле:
.
Инвариантность qF к условиям резания объясняется тем, что металл в прирезцовых слоях стружки достигает предельную степень деформации.
В ряде работ также показано, что qF не зависит от температуры и является характеристикой только обрабатываемых материалов.
Если считать, что нормальные напряжения изменяются по закону треугольника, расчет ширины площадки контакта можно производить по формуле:
С = 2 а cos n/ [ tg ( b + n – g) sin b cos (b – g)] ,
где n – угол трения на передней поверхности инструмента (рис. 4.10).
Таким образом, ширины площадки контакта (С) уменьшается с возрастанием углов сдвига и трения. При свободном резании с углом l = 0 силы N и F можно определить (см. рис. 4.10), если будут известны действующие на разрезаемый слой сила 
, совпадающая с вектором скорости резания, и сила 
, ей перпендикулярная (эти силы можно определить динамометрированием).
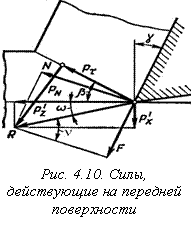
Равнодействующая этих сил является силой стружкообразования (R), наклоненной к направлению резания под углом действия:
w = arctg 
.
На основании рисунка 4.10 имеем:
N = cos (w + g) / cos w;
F = sin(w + g) / cos w;
Средний коэффициент трения, вычисленный по закону трения Амонтона-Кулона:
m = F/N = tg (w + g).
Таким образом, между углом трения (n) на передней поверхности, передним углом инструмента и углом действия существует зависимость:
n = w + g.
С увеличением среднего коэффициента трения при неизменном переднем угле угол действия растет, и увеличивается его влияние на деформационные процессы в срезаемом слое. В частности, зависимость между углами b, n, w и g можно описать с помощью формулы К.А. Зворыкина:
2b + n – g = 2b + w = с,
где с – постоянная величина, близкая к 80°.
Увеличение средних нормальных контактных напряжений приводит к снижению m, и наоборот. Значение m при резании достигает 1,2…3. Это позволяет дать физическое объяснение возникновению зоны вторичной деформации стружки. Сила схватывания между опорной поверхностью стружки и лезвием во многих случаях превышает силу сопротивления движению стружки в слое, лежащем в ее толще.
Граничные слои затормаживаются, а основной объем перемещается в продольном направлении за счет внутренних сдвигов. Эти сдвиги являются вторичной пластической деформацией стружки и сопровождаются дальнейшим упрочнением деформируемых слоев, начиная со слоя, ближайшего к опорной поверхности стружки. При достижении в каждом слое стружки силы сопротивления сдвиговым деформациям, равной силе схватывания опорной поверхности стружки с инструментом, вся стружка в целом будет перемещаться относительно передней поверхности инструмента.
На коэффициент трения оказывают влияние физико-механические и теплофизические свойства обрабатываемого материала, передний угол (g), толщина среза (а), скорость резания (V) и применяемое смазочно-охлаждающее технологическое средство (СОТС).