Здесь мы покажем, как применяются ряды Фурье при решении задачи о колебании струны. Под струной мы понимаем тонкую гибкую нить, не оказывающую сопротивления изгибу.
Рассмотрим струну, которая в начальный момент совмещена с отрезком ![]() оси Ох. Будем считать, что концы х = 0 и x = l закреплены на оси Ох. Пусть струна растягивается силами
оси Ох. Будем считать, что концы х = 0 и x = l закреплены на оси Ох. Пусть струна растягивается силами ![]() и
и ![]() , приложенными к её концам и направленными вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить самой себе, под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдет дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна станет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.
, приложенными к её концам и направленными вдоль оси Ох. Если струну вывести из состояния равновесия и затем предоставить самой себе, под влиянием растягивающих сил точки струны придут в движение, стремясь вернуться в исходное положение. Придя в это положение, каждая точка струны будет обладать уже некоторой скоростью и по инерции пройдет дальше своего равновесного положения. При этом дальнейшем движении точек они будут тормозиться растягивающими силами и т.д. Таким образом, струна станет совершать некоторое колебательное движение. Задача состоит в исследовании этого движения.
Сделаем ряд предположений. Во-первых, считаем, что, выводя струну из состояния равновесия, мы придаем ей форму некоторой линии. Поскольку концы струны закреплены на оси Ох, то на функцию U(x) линии надо наложить требования U(0) = U(l) = 0. Во-вторых, будем предполагать, что каждая точка струны совершает только поперечные колебания, перпендикулярные оси Ох. В-третьих, колебания предположим малыми, что квадратами отклонений точек струны от оси Ох можно пренебречь. Кроме того, будем считать, что во все время движения струна будет сохранять пологую (гладкую) форму, это значит, что угол ![]() , образуемый касательной к струне с осью Ох, мал, чтобы можно было считать
, образуемый касательной к струне с осью Ох, мал, чтобы можно было считать ![]() . Наконец, считаем струну однородной, причем массу единицы длины струны в её нерастянутом состоянии считать равной её плотности
. Наконец, считаем струну однородной, причем массу единицы длины струны в её нерастянутом состоянии считать равной её плотности![]() .
.
Возьмем какую-либо точку струны, имевшую в начальный момент t = 0 абсциссу х. Так как эта точка будет двигаться перпендикулярно оси Ох, то во время движения её абсцисса х не будет меняться. Ордината её у будет зависеть от времени, а также от того, о какой точке идет речь, а именно от абсциссы х этой точки, т.е. ордината будет функцией от х и t. Эту функцию в дальнейшем будем обозначать через U(x, t). Ясно, что она должна удовлетворять граничным условиям:
![]() (1.9)
(1.9)
и начальным условиям:
![]() (1.10)
(1.10)
первое из (4.10) выражает, что струне придана форма, а второе означает, что точки струны имеют начальные скорости (мы, предположим, что ![]() ).
).
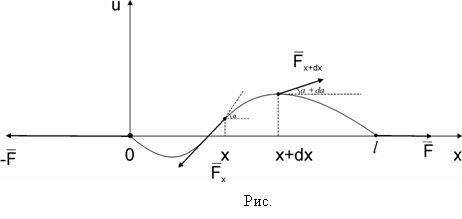
Переведем физическую задачу на язык математики, т.е. выведем дифференциальное уравнение, которому должна удовлетворять искомая функция U(x,t). Для этого выделим на струне элементарный участок, который при t = 0 совпадает с отрезком [x,x+dx] оси Ох. В момент t это будет дуга линии U(x ,t). Длина этой дуги:
![]() ,
,
 |
пренебрегая ![]() (мы сделали допущение, что
(мы сделали допущение, что ![]() ), получим: ds = dx (т.е. струна не растягивается). Масса выделенного участка равна:
), получим: ds = dx (т.е. струна не растягивается). Масса выделенного участка равна: ![]() . К этому элементу будут приложены растягивающие его силы. Пусть натяжение в точке х будет равно
. К этому элементу будут приложены растягивающие его силы. Пусть натяжение в точке х будет равно ![]() . Тогда к концам нашего элемента будут приложены силы
. Тогда к концам нашего элемента будут приложены силы ![]() и
и ![]() .
.
Они направлены по касательным в этих точках. Обозначим через ![]() и
и ![]() соответствующие углы в точках струны (рис. 4.1). Обозначим равнодействующую сил, приложенных к концам элемента, через
соответствующие углы в точках струны (рис. 4.1). Обозначим равнодействующую сил, приложенных к концам элемента, через ![]() , а ускорение элемента через
, а ускорение элемента через ![]() . Тогда векторное уравнение движения элемента имеет вид:
. Тогда векторное уравнение движения элемента имеет вид:
![]() . (4.11)
. (4.11)
Спроектируем это уравнение на ось Ох, находим:
![]() (4.12)
(4.12)
(![]() означает проекцию силы
означает проекцию силы ![]() на ось Ох, а
на ось Ох, а ![]() – численные значения натяжения в точке, абсцисса которой х).
– численные значения натяжения в точке, абсцисса которой х).
Поскольку точки струны движутся перпендикулярно оси Ох, то ![]() , стало быть
, стало быть ![]() . Но
. Но
![]()
так как ![]() . Сопоставляя это с равенством
. Сопоставляя это с равенством ![]() , находим, что
, находим, что ![]() . Это значит, что величина натяжения не меняется вдоль струны. Но, так как на концах струны это натяжение есть
. Это значит, что величина натяжения не меняется вдоль струны. Но, так как на концах струны это натяжение есть ![]() , вместо Fx, Fx=dx будем писать:
, вместо Fx, Fx=dx будем писать: ![]() .
.
Спроектируем уравнение (4/11) на ось Оу:
![]() (4.13)
(4.13)
Так как ![]() , а
, а ![]() то (4.13) дает:
то (4.13) дает:
![]()
но ![]() Отсюда
Отсюда 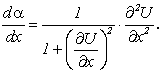
Пренебрегая ![]() , получим:
, получим: ![]()
Тогда уравнение будет иметь вид:
![]() (4.14)
(4.14)
где ![]() . Уравнение (4.14) называется уравнением свободных колебаний струны или волновым уравнением.
. Уравнение (4.14) называется уравнением свободных колебаний струны или волновым уравнением.
Таким образом, механическая задача свелась к чисто математической (получили математическую модель процесса колебания струны): найти такое решение уравнения (4.14), которое удовлетворяет начальным и граничным условиям (4.9) и (4.10). Существуют разные способы решить эту задачу. Один из способов был предложен в XYIII веке Д. Бернулли. Позже, уже в XIX веке, этот способ систематически применялся Фурье для решения целого ряда термодинамических задач, почему он и получил название метода Фурье. Этот способ мы рассмотрим далее. Он требует сначала решения одной важной задачи, которая носит название задачи о собственных значениях и собственных функциях. Однако решим одну вспомогательную задачу: найти функцию U = U(x, t), удовлетворяющую требованиям:
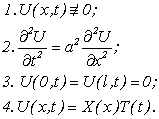 (4.15)
(4.15)
Отличие этой задачи от той, которую нам надо решить, состоит в том, что от искомой функции U(x ,t) мы не требуем, чтобы она удовлетворяла начальным условиям где ![]() , но зато требуем, чтобы она имела специальный вид X(x)T(t) и была отличной от тождественного нуля.
, но зато требуем, чтобы она имела специальный вид X(x)T(t) и была отличной от тождественного нуля.
Измененная задача решается довольно просто и имеет бесконечное множество решений, из которых удается составить и решение нашей основной задачи.
Итак, пусть имеем первое условие (4.15). Из него вытекает, существование такой точки ![]() , что
, что ![]() . Тогда
. Тогда ![]() , т.е.
, т.е. ![]() . Подставим
. Подставим ![]() в граничные условия:
в граничные условия: ![]()
Отсюда видно, что искомая функция X(x) должна удовлетворять условиям:
X(0) = X(l) = 0. (4.16)
Подставляя из четвертого условия (4.15.) ![]() во второе, получим:
во второе, получим:
![]() , т.е.
, т.е. ![]() . (4.17)
. (4.17)
Обратим внимание, на то, что правая часть (4.15) не зависит от ![]() . Следовательно, и левая часть от
. Следовательно, и левая часть от ![]() не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного
не должна зависеть. С другой стороны, эта левая часть может быть функцией только одного ![]() , ибо
, ибо ![]()
![]() . Значит, левая (и правая) часть равенства должна быть постоянной величиной. Обозначим ее (пока неизвестную) через
. Значит, левая (и правая) часть равенства должна быть постоянной величиной. Обозначим ее (пока неизвестную) через ![]() .
.
Допустим, что ![]() . Тогда из (4.17) следует
. Тогда из (4.17) следует ![]() . Отсюда
. Отсюда ![]() и
и ![]() , т.е.
, т.е. ![]() должна быть линейной функцией. Подставляя
должна быть линейной функцией. Подставляя ![]() в X(0 )= X(l) = 0, получим:
в X(0 )= X(l) = 0, получим:
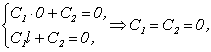
т.е. ![]() , а с ним и
, а с ним и ![]() , что противоречит допущению первому из (4.15). Таким образом, не существует решения вспомогательной задачи для
, что противоречит допущению первому из (4.15). Таким образом, не существует решения вспомогательной задачи для ![]()
![]() .
.
Допустим, что ![]() , т.е.
, т.е. ![]() , где
, где ![]() можно считать положительным. Тогда
можно считать положительным. Тогда
![]() .
.
Общее решение этого уравнения имеет вид:
![]() .
.
Используя граничные условия X(0) = X(l) = 0, получим:
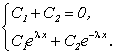
Решая эту систему, находим ![]() . Это приводит к
. Это приводит к ![]() , что противоречит первому условию (4.15). Итак, неравенство
, что противоречит первому условию (4.15). Итак, неравенство ![]() невозможно.
невозможно.
Пусть ![]() , т.е.
, т.е. ![]() , где
, где ![]() . Тогда
. Тогда
![]() .
.
Решив это уравнение, получим:
![]() . (4.18)
. (4.18)
Граничные условия дают: ![]() . Заменяя
. Заменяя ![]() на С, имеем
на С, имеем ![]()
![]() , а второе условие дает
, а второе условие дает ![]() . Это возможно лишь при
. Это возможно лишь при ![]() . Значит, для
. Значит, для ![]() возможны значения
возможны значения ![]() , что приводит к следующим выражениям для
, что приводит к следующим выражениям для ![]() :
:
![]()
![]() , (4.19)
, (4.19)
причем ![]() при каждом
при каждом ![]() может принять любое (отличное от 0) значение. Заметим, что здесь решена задача о собственных значениях и собственных функциях. Поэтому числа
может принять любое (отличное от 0) значение. Заметим, что здесь решена задача о собственных значениях и собственных функциях. Поэтому числа ![]() и функции
и функции ![]() называются соответственно: собственными числами, а функции собственными функциями, которые соответствуют собственным числам (значениям).
называются соответственно: собственными числами, а функции собственными функциями, которые соответствуют собственным числам (значениям).
Выбрав возможное значение ![]() , и подставив в (4/17), получим:
, и подставив в (4/17), получим:
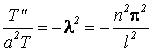
т.е.
![]() , (4.20)
, (4.20)
где А и В – произвольные постоянные. Обозначая Т буквой Тn и полагая ![]() ,
, ![]() , получаем бесконечное множество решений вспомогательной задачи:
, получаем бесконечное множество решений вспомогательной задачи:
![]() . (4.21)
. (4.21)
Отметим, что наше уравнение и условия ![]() линейны и однородны, т.е. такие, что сумма функций
линейны и однородны, т.е. такие, что сумма функций ![]() , которая удовлетворяет им, также будет решением. Поэтому функция
, которая удовлетворяет им, также будет решением. Поэтому функция
![]() (I.3.14)
(I.3.14)
при условии сходимости ряда также будет решением. Чтобы функция (4.22) была решением исходной задачи надо подобрать ![]() и
и ![]() так, чтобы выполнялись начальные условия (4.10).
так, чтобы выполнялись начальные условия (4.10).
Первое условие с (4.10) дает:
![]() . (4.23)
. (4.23)
Дифференцируя (4.22), получим:
![]() . (4.24)
. (4.24)
Чтобы удовлетворить соотношению (4.24), надо положить ![]() . Соотношение (4.23) говорит, что коэффициенты
. Соотношение (4.23) говорит, что коэффициенты ![]() должны равняться коэффициентам разложения функции
должны равняться коэффициентам разложения функции ![]() , заданной на [0,l], по функциям
, заданной на [0,l], по функциям ![]() в ряд Фурье. Поэтому
в ряд Фурье. Поэтому
 . (4.25)
. (4.25)
Таким образом, искомое решение имеет вид
![]() (4.26)
(4.26)
где ![]() определяется по (4.25).
определяется по (4.25).
Замечания
1) Полученное решение носит формальный характер, так как мы не исследовали сходимость ряда (4.26). Однако можно показать, что если функция ![]() гладкая на [0,l], то ряд сходится и его сумма U(x,t) удовлетворяет исходному уравнению и начальным и краевым условиям.
гладкая на [0,l], то ряд сходится и его сумма U(x,t) удовлетворяет исходному уравнению и начальным и краевым условиям.
2) Примененный метод решения задачи обычно называют методом Фурье или методом разделения переменных или методом собственных функций.
Решение (4.22) с учётом ![]() ,
, ![]() можно записать в виде:
можно записать в виде:
![]() (4.27)
(4.27)
Каждый член этого ряда представляет собой так называемую стоячую волну, при которой точки струны совершают гармоническое колебательное движение с одинаковой фазой ![]() , с амплитудой
, с амплитудой ![]() и частотой
и частотой ![]() .
.