Задан массив узлов, аппроксимирующих заданный закон изменения выходной координаты системы х₃ = f (t). Известны структура последовательной цепочки звеньев с выходными координатами х₁, x₂ и х₃  и численные значения их параметров, приведенные выше. Задан закон изменения внешнего воздействия на вход системы и = kt.

Требуется определить дополнительное входное воздействие на вход первого звена, осуществляемое обратными связями и реализующее заданный закон изменения выходной координаты х₃, а по нему найти число, вид, место включения и параметры обратных связей.

Расчетные уравнения для рассматриваемой задачи в соответствии с уравнениями (4.1) будут иметь вид

Δx₃,_i = x₃,_i – x₃,_i-1,

x₂,_i = 2T₂Δx_3,i  / (k₄ Δt) + 2x₃,_i-1 / k₄ – x₂,_i-1;

Δx₂,_i = x_2,i – x_2,i-1;

x₁,_i = 2T₁ Δx₂,_i / (k₃ Δt) + 2x_2,i-1 / k₃ x₁,_i-1;

Δx_1,i = x_1,i – x_1,i-1;

Σ x_1,m,i = Δx_1,i  / (k₁Δt) – (u_i-1 — kΔt / 2).

Структурная схема алгоритма синтеза для решения рассматриваемой задачи приведена на рис. 4.6.

Процедура вычислений заключается в следующем.

1) Вводятся (оператор 1) исходные данные, описанные в предыдущей задаче. Однако в связи с изменением постановки задачи в исходные данные вместо информации об обратной связи (коэффициент k₂) вводится информация о внешнем входном воздействии на систему (коэффициент k).

2) Операции, выполняемые операторами 2 – 6, остаются прежними, описанными в предыдущей задаче.

3) Поскольку в рассматриваемой задаче функция и (t) на входе системы известна, то логический оператор 7 осуществляет переход к оператору 11.

4) Оператор 11 обеспечивает вычисление искомых воздействий обратных связей по последнему уравнению системы (4.8).

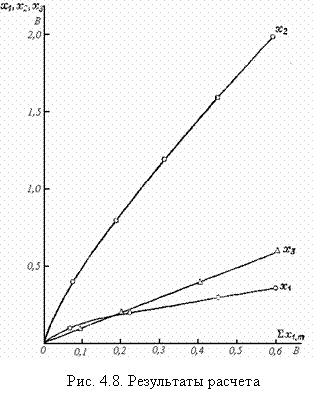
5) Оператор 12 обеспечивает нахождение места включения и характеристику обратной связи. В диалоговом режиме эта операция осуществляется вычислением и выводом на дисплей зависимостей X_1,i = f(ΣX_1,m,i), X_2,i = f(ΣX_1,m,i), X_3,i = f(ΣX_1,m,i) и анализом инженером-оператором получаемых характеристик с точки зрения их реализуемости. В рассматриваемом примере дополнительное воздействие на вход первого звена от обратных связей реализуется одной линейной связью по выходной координате X₃.

6) Оператор 13 обеспечивает вычисление коэффициента обратной связи по уравнению

ko_c = ΣX_1,m,i / X_3,i.

7) Дальнейшие операции, осуществляемые операторами 9 и 10, аналогичны описанным в предыдущей задаче. В операторе 9 на устройство печати выводятся значения характеристики обратной связи в определенных точках и коэффициента обратной связи.

В рассматриваемой задаче для наглядности на дисплей и устройство печати были выведены все три зависимости X₁, X₂, X₃. Эти зависимости приведены на рис. 4.8. Из этого рисунка видно, что дополнительное воздействие может быть реализовано с помощью лишь одной связи по координате, причем по координатам X₁ и X₂ – нелинейными связями, а по координате Х₃ – линейной. Последняя, как наиболее просто реализуемая, принимается за искомое решение. Коэффициент обратной связи k₂ = 1.