Задан массив узлов, аппроксимирующий заданный закон изменения выходной координаты системы x3 = f (t). Известны структура, численные значения параметров первого и третьего звеньев, а также внешнее воздействие на вход системы и = kt и коэффициент обратной связи k2. Известные параметры системы имеют численные значения, приведенные выше.
Требуется определить значения параметров второго звена T1 и k3, реализующие при поставленных условиях закон изменения выходной координаты системы x3 = f(t).
Задача решается, как указывалось ранее, ходом «справа» и «слева».
Структурная схема алгоритма параметрического синтеза приведена на рис. 4.9. Процедура вычислений заключается в следующем.
1) Вводятся (оператор 1) исходные данные, описанные в первой задаче. Однако в связи с изменением постановки задачи не вводится информация о параметрах второго звена, нo дополнительно вводится значение коэффициента k, определяющего внешнее входное воздействие на систему.
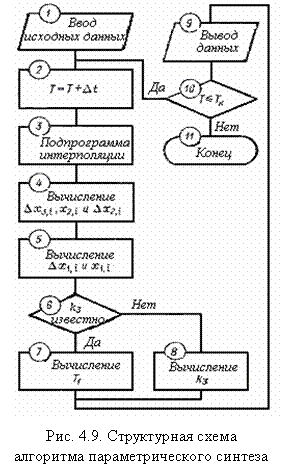2) Оператор 2 осуществляет вычисление текущего времени счета.
3) Подпрограмма интерполяции (оператор 5) осуществляет вычисление значений координаты х3 в точках, отличных от узлов интерполяции.
4) Оператор 4 обеспечивает вычисление ΔX3,i , X2,i , ΔX2,i (ход «справа»).
5) Оператор 5 обеспечивает вычисление ΔX1,i и X1,i (ход «слева»).
6) Логический оператор 6 определяет дальнейший ход решения задачи. Если k3 – коэффициент усиления второго звена известен, то осуществляется переход к оператору 7 для вычисления постоянной времени звена T1. В противном случае осуществляется переход к оператору 8.
7) Значение k3 может быть известно либо задано оператором. При решении поисковых вариационных задач вводится массив возможных значений коэффициента ks в желаемом или возможном диапазоне его изменения и определяется соответствующий ему массив значений T1 (оператор 7). Из всех возможных значений k3 выбирается наиболее приемлемое и легко физически реализуемое. В диалоговом режиме эта операция осуществляется человеком-оператором. Значение Т1 вычисляется по формуле
T1 = (Δt / ΔX2,i) [X1,i-1 +ΔX1,i / 2) k3 – X2,i-1].
8) Если значение k3 является искомым, то задаются значения величины Т1, а осуществляется вариационный поиск k3 (оператор 8) аналогично описанному выше.
9) Оператор 9 обеспечивает вывод данных на устройство печати, а оператор 10 зацикливает программу расчета или обеспечивает ее окончание.
 |
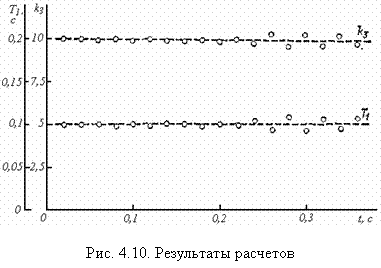На рис. 4.10 приведены результаты расчетов, полученные при решении поставленной задачи.
Во всех трех задачах синтеза получены результаты, согласующиеся со структурой и параметрами исходной системы. Рассмотренный пример, носящий несколько абстрактный характер, имеет целью наглядно проиллюстрировать практическое применение инверсного метода синтеза АСУ, процедуру вычислений и достоверность получаемых результатов.