Определение 1

Дерево, имеющее n вершин, называется нумерованным, если каждой из его вершин присвоен индивидуальный номер kÎ{1, 2, …, n}.

Теорема 1 (Кэли)

Число нумерованных деревьев с n вершинами равно n^n-2.

Доказательство

Сопоставим каждому нумерованному дереву последовательность n – 2 чисел принадлежащих {1, 2,×…,n}. Эта последовательность называется кодом Прюфера и строится следующим образом. В цикле находится висячая вершина с наименьшим номером. Номер вершины, смежной с найденной, записывается в последовательность. Цикл повторяется n - 2 раза. Наоборот, по последовательности n чисел из {1, 2,…,n + 2} можно построить нумерованное дерево с помощью следующих действий:

1) выписываем множество:

B = {1, 2, 3, … ∙, n + 2};

2) устанавливаем начальное множество ребер дерева T = Æ;

3)

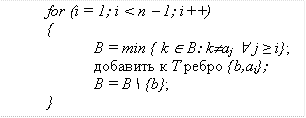далее выполняются действия:

Число последовательностей из n – 2 чисел принадлежащих множеству {1, 2, …∙, n} равно n^n-2, значит, число нумерованных деревьев равно n^n-2.

Доказательство следующего утверждения можно найти в [3].

Пусть Г – граф. Его поддеревом T  называется подграф, который является деревом. В этом случае мы будем говорить также, что T содержится в графе Г. Поддерево T графа Г называется максимальным, если оно не содержится ни в каком отличном от него поддереве T’ графа Г.

Теорема 2

Число максимальных поддеревьев связного графа равно абсолютной величине алгебраического дополнения произвольного элемента матрицы:

,

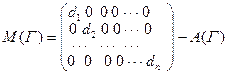где d_i – степени вершин графа G, A(G) =( a_{i j} ) – матрица смежности

Пример 1

Рассмотрим граф G (рис. 4.5). Вычислим количество его максимальных поддеревьев.

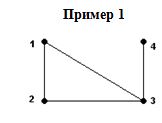
Рис. 4.5. Простой граф

Найдем матрицу M(G):

.

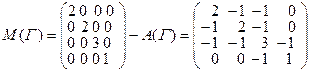Отсюда число максимальных поддеревьев равно |A₃₁| = 3.