Пусть Е = Е₁?Е₂?…?Е_n – прямое произведение универсальных множеств и М – некоторое множество принадлежностей (например, М = [0,1]). Нечеткое n-арное отношение определяется как нечеткое подмножество R на E, принимающее свои значения в М. В случае n=2 и М = [0,1], нечетким отношением R между множествами X = Е₁ и Y = Е₂ будет называться функция RX, Y)® [0,1], которая ставит в соответствие каждой паре элементов (х, y)IX?Y величину m_R(x, y) I[0,1]. Обозначение: нечеткое отношение на X?Y запишется в виде: xIX, yIY: xRy. В случае, когда X = Y, т.е. X и Y совпадают, нечеткое отношение R: X?X®[0,1] называется нечетким отношением на множестве X.

Примеры:

1) Пусть X = {x₁, x₂, x₃}, Y = {y₁, y₂, y₃, y₄}, М = [0,1]. Нечеткое отношение R = XRY может быть задано, к примеру, табл. 4.3.

Таблица 4.3

Задание нечеткого отношения

2) Пусть X = Y =, т.е. множество всех действительных чисел. Отношение  (x много больше y) можно задать функцией принадлежности:

3) Отношение R, для которого m_R(x, y) = , при достаточно больших k можно интерпретировать так: "x и y – близкие друг к другу числа". В случае конечных или счетных универсальных множеств очевидна интерпретация нечеткого отношения в виде нечеткого графа, в котором пара вершин (x_i, x_j) в случае XRX соединяется ребром с весом m_R(x_i, x_j), в случае XRY пара вершин (x_i, y_j) соединяется ребром c весом m_R(x_i, y_j).

4) Пусть Х = {x₁, x₂, x₃}, и задано нечеткое отношение R: X´X® [0,1], представленное графом (рис. 4.9).

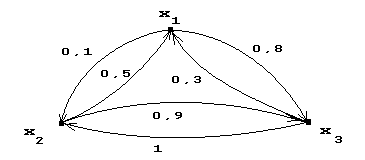
Рис. 4.9. Граф нечеткого отношения R для примера 4

5) Пусть X = {x₁, x₂} и Y = {y₁, y₂, y₃}, тогда нечеткий граф (рис. 4.10) задает нечеткое отношение XRY.

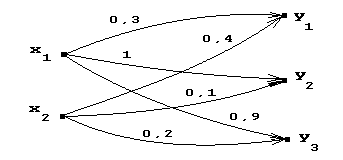
Рис. 4.10. Нечеткий граф для примера 5

Замечание. В общем случае нечеткий граф может быть определен на некотором GÌX´Y, где G – множество упорядоченных пар (x, y) (необязательно всех возможных) такое, что GÇ = Æ и GÈ = X´Y.

Будем использовать обозначения  вместо  и  вместо

Пусть R: X´Y®[0,1].