Чаще всего риск на практике оценивают на основе сравнения с наилучшими достигнутыми результатами. В зависимости от масштаба изучаемой системы эти сравнительные оценки могут выглядеть по-разному. Например, в таблице 4.1 представлены сравнительные данные риска смертельного производственного травматизма для стран и групп стран мира, различающихся по уровню развития.

Естественно, что нас интересует позиционирование нашей страны. Россия имеет примерно такой же уровень риска, как и бывшие социалистические страны, Китай, Индия, но риск смертельного производственного травматизма в России в три раза выше, чем в развитых странах. Однако этот уровень, которым мы недовольны, пока недостижим для стран Ближнего Востока и Африки.

Таблица 4.1 Сравнение риска смертельного производственного травматизма для стран и групп стран мира (2002 г.)

В данном случае критерием оценки является наилучший достигнутый результат. Для того, чтобы контролировать тенденции и эффективность мероприятий, предпринимаемых по достижению лучших результатов, рассматривают динамику процесса (изменение ситуации во времени). В таблице 4.2 представлена динамика показателей травматизма в России за период с 1975 по 2010 гг.

Таблица 4.2 Динамика показателей травматизма в России за период с 1975 по 1995 гг.

Как следует из представленных данных, динамика положительная, и при ее сохранении Россия сможет добиться лучших мировых показателей через несколько лет.

Для оценки ситуации на исследуемой территории сравнивают показатели травматизма в стране, округе, крае, городе. Например, в  таблице 4.3 представлены сравнительные данные по показателям общего и смертельного производственного травматизма в РФ, Дальневосточном федеральном округе, Хабаровском крае, г. Комсомольске-на-Амуре. Для Дальневосточных территорий критерием оценивания риска травматизма являются показатели РФ.

Таблица 4.3 Сравнение риска производственного травматизма по территориям за 2009 г.

Среднемноголетние уровни показателей травматизма (R_{ср мн}) также могут рассматриваться как критерии для сравнения, оценивания и принятия решений (рис. 4.1). Тренд (от англ. Trend – тенденция) – общая тенденция при разнонаправленном движении, выраженная общая направленность изменений показателей любого временного ряда. Графики могут быть описаны различными уравнениями – линейными, логарифмическими, степенными и т.д. Фактический тип графика устанавливают на основе графического изображения данных временного ряда, путем осреднения показателей динамики ряда, на основе статистической проверки гипотезы о постоянстве параметров графика.

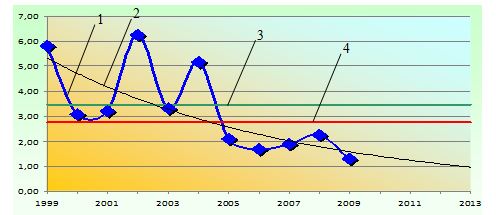
Рис. 4.1. Динамика коэффициента частоты травматизма (1), экспоненциальный тренд (2), среднемноголетние уровни на предприятии (3) и в отрасли (4)

Линии тренда  позволяют графически отображать тенденции данных и прогнозировать данные. Подобный анализ называют также – регрессионный анализ. Регрессионный анализ – вид статистического анализа, используемый для прогнозирования. Регрессионный анализ позволяет оценить степень связи между переменными, предлагая механизм вычисления предполагаемого значения переменной из нескольких уже известных значений.

Используя регрессионный анализ, можно продлить линию тренда в диаграмме за пределы реальных данных для предсказания будущих значений.

Линия тренда может быть подобрана в Excel. Наиболее надежной считается линия тренда, у которой значение R² равно 1 или близко к 1; R², или показатель определенности, – это число от 0 до 1, которое означает близость значений линии тренда к фактическим данным. Чем больше эта величина, тем достовернее линия тренда. При подборе линии тренда к данным Excel автоматически рассчитывает R².

Можно выбрать любой из следующих типов линии тренда: линейную, полиномиальную, логарифмическую.

Линейная используется для линейной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

,

где m – угол наклона и b – координата пересечения оси абсцисс.

Линейная аппроксимация – это прямая линия, наилучшим образом описывающая набор данных. Она применяется в самых простых случаях, когда точки данных расположены близко к прямой.

Полиномиальная используется для полиномиальной или криволинейной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

,

где c₁,… c₆ и b – константы.

Полиномиальная аппроксимация используется для описания величин, попеременных возрастающих и убывающих. Она полезна, например, для анализа большого набора нестабильных величин. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой.

Логарифмическая используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

,

где c и b – константы; ln – функция натурального логарифма.

Логарифмическая аппроксимация хорошо описывает величину, которая вначале растет или убывает, а затем постепенно стабилизируется. Описывает как положительные, так и отрицательные величины.

Степенная используется для степенной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

,

где c и b – константы.

Если в данных имеются нулевые или отрицательные значения; использование степенного приближения невозможно,

Экспоненциальная используется для экспоненциальной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

,

где c и b – константы, e – основание натурального логарифма.

Для данных, которые содержат нулевые или отрицательные значения, этот вид приближения неприменим.

Скользящее среднее (линейная фильтрация) используется для создания скользящего среднего в соответствии с уравнением:

.

Использование в качестве приближения скользящего среднего позволяет сгладить данные и, таким образом, более наглядно показать характер зависимости. Такая линия строится по определенному числу точек (оно задается параметром «Шаг»). Элементы усредняются, и полученный результат используется в качестве среднего значение приближения. Так, если «Шаг» равен 2, первая точка сглаживающей кривой определяет среднее значение первых двух элементов данных, вторая точка – как среднее следующих двух элементов, и так далее. Для скользящего среднего значение R² не может быть отображено.