Рассмотрим систему управления, состоящую из двух  апериодических и одного интегрирующего звеньев, охваченных отрицательной обратной связью.

Расчетные уравнения для анализа рассматриваемой системы будут иметь следующий вид:

^{ΔX 1,I = [(ui-1+Δui  / 2)-k2X3,i-1] k1Δt;}

^{ΔX 2,i = [(X1,I-1 + ΔX 1,I  / 2) k3  — X 2,I-1] Δt / T1;}

^{X2,I = X2,I-1  +   ΔX2,I;}

^{ΔX3,I = (Δt / T2 ) [(X2,I-1 + ΔX 2,I  / 2) k1  — X 3,I-1];}

^{X3,I = X3,I-1 +  ΔX3,I.}

Численные значения параметров системы и исходных данных для расчета процессов в системе имеют следующие значения:

u = kt,   k = 10,  k₁ = 1,

k₂ = 1, k₃ = 10, k₄ = 0,5, T₁ = 0,1 c,

T₂ = 0,08 c,  Δt = 0,02 c.

Начальные условия для всех переменных приняты для простоты нулевыми, т. е. при t = 0

u_о = x_{1, 0}  = x₂, ₀  =  х_з,0  = 0.

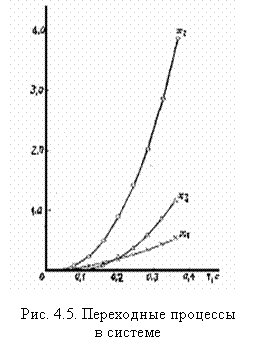
Тогда переходные процессы в рассматриваемой системе, рассчитанные по уравнениям (4.6), будут иметь вид графиков, приведенных на рис. 4.5.