Рассмотрим задачу перечисления бинарных деревьев. Введем определения.

Определение 1

Дерево с выделенной вершиной называется корневым, а выделенная вершина – его корнем (рис. 4.6). Для каждой вершины q существует единственный элементарный путь, соединяющий ее с корнем. Длина этого пути называется высотой вершины q. Смежные с q вершины, высота которых больше высоты вершины q  на 1, называются детьми вершины q. На рис. 4.6 показано дерево с корнем 3.

Определение 2

Корневое дерево, каждая вершина которого имеет не более двух детей, называется бинарным, если детям приписан дополнительный признак «левой» или «правой» смежной вершины. Вершина не может иметь две левые или две правые смежные вершины. Бинарное дерево вместе с функцией, сопоставляющей каждой вершине некоторое число, называется бинарным деревом чисел.

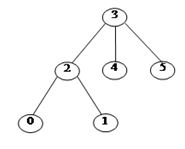
Рис. 4.6. Корневое дерево

Бинарное дерево чисел можно определить по индукции:

1) пустое дерево является бинарным деревом чисел;

2) если T₁ и T₂ – бинарные деревья чисел, то (T₁, некоторое число, T₂) – бинарное дерево чисел.

Определим отношение эквивалентности на множестве бинарных деревьев чисел S~T следующим образом:

1) если S = T = Æ,    то S~T;

2) если S = (S₁, m, S₂),  T = (T₁, n, T₂),  S₁~ T₁  и S₂~ T₂,     то S~T.

Число классов эквивалентности бинарных деревьев имеющих n вершин называется n-м числом Каталана и обозначается через c_n .

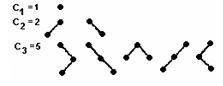
Рис. 4.7. Бинарные деревья

На рис. 4.7 показаны классы эквивалентности бинарных деревьев, имеющих n вершин, при n = 0, 1, 2, 3.

Пример 1 (число расстановок скобок)

Пусть ‘*’ — бинарная операция на множестве A, которая не предполагается ни коммутативной, ни  ассоциативной. Введем определение для алгебраических выражений, составленных с помощью этой операции, скобок и букв. Такие выражения определим с помощью индукции, и будем называть их термами:

1) для всякого элемента a Î A слово a есть терм;

2) если t₁ и t₂ – термы, то (t₁* t₂) – терм.

В нормальной форме Бэкуса-Наура определение будет следующим:

Терм ::=  a | (Терм*Терм).

Здесь a Î A – произвольный элемент. Например, термами являются слова: (a*a)*b, a*(b*c), и т.д. Число термов, содержащих n операций *, равно c_n.

Бинарным деревьям (см. рис. 4.7) соответствуют термы:

1) a;

2) (a*b);

3) ((a*b)*c), (a*(b*c));

4) (a*((b*c)*d)),  (a*(b*(c*d))), ((a*b)*(c*d)), (((a*b)*c)*d), ((a*(b*c))*d).

Пример 2

Деревом поиска называется бинарное дерево, вершинам которого соответствуют элементы некоторого линейно упорядоченного множества. Причем для каждой вершины значение в ней не меньше значений в вершинах левого поддерева и больше значений в вершинах правого поддерева. Элементы возрастающей последовательности n чисел можно расположить в узлах дерева поиска. Оно будет бинарным деревом и может быть выбрано c_n способами.

Теорема 1

Числа Каталана равны .

Доказательство

Имеют место соотношения для чисел классов бинарных деревьев:

c_k = c₀c_k-1 + c₁c_k-2 + … +c_k-1c₀, для всех k > 0.

Пусть C(x) =  — производящая функция последовательности чисел Каталана.

Получаем:

C(x) = xC²(x) + 1,

откуда

.