Используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:

;

;

     …….…………………………………

,

где – входная переменная (имя для известных значений данных); – переменная вывода (имя для значения данных, которое будет вычислено);  и – функции принадлежности, определенные на  и .

Пример подобного правила:

Если x – низко, то y – высоко.

Приведем более детальное пояснение. Знание эксперта  отражает нечеткое причинное отношение предпосылки и заключения, поэтому его можно назвать нечетким отношением и обозначить через R:

,

где «» называют нечеткой импликацией.

Совокупность импликаций  отражает функциональную взаимосвязь входных и выходных переменных и является основой построения нечеткого отношения , заданного на произведении  универсальных множеств входных и выходных переменных. Если на множестве  задано нечеткое множество , то композиционное правило вывода  определяет на  нечеткое множество  с функцией принадлежности

,

где – операция выбора наибольшего по  значения.

Таким образом, процесс получения нечеткого результата вывода  с использованием данного наблюдения  и знания  можно представить в виде композиционного правила нечеткий «modus ponens»:

,

где «»– операция свертки.

Как операцию композиции, так и операцию импликации в алгебре нечетких множеств можно реализовать по-разному (при этом будет отличаться и получаемый результат), но в любом случае общий логический вывод осуществляется, как правило, за следующие четыре этапа.

1) Введение нечеткости (фаззификация). Функции принадлежности, определенные на входных переменных, применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила.

Логический вывод. Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила. Это приводит к одному нечеткому подмножеству, которое будет назначено каждой переменной вывода для каждого правила. В качестве правил логического вывода обычно используются только операции (минимум) или (умножение). В логическом выводе минимума

1) функция принадлежности вывода «отсекается» по высоте, соответствующей вычисленной степени истинности предпосылки правила (нечеткая логика «И»). В логическом выводе умножения функция принадлежности вывода масштабируется при помощи вычисленной степени истинности предпосылки правила.

2) Композиция. Все нечеткие подмножества, назначенные к каждой переменной вывода (во всех правилах), объединяются вместе, чтобы формировать одно нечеткое подмножество для каждой переменной вывода. При подобном объединении обычно используются операции  (максимум) или  (сумма). При композиции максимума комбинированный вывод нечеткого подмножества конструируется как поточечный максимум по всем нечетким подмножествам (нечеткая логика «ИЛИ»). При композиции суммы комбинированный вывод нечеткого подмножества формируется как поточечная сумма по всем нечетким подмножествам, назначенным переменной вывода правилами логического вывода.

3) Приведение к четкости, дефаззификация. Используется, когда полезно преобразовать нечеткий набор выводов в четкое число.

Пример. Пусть некоторая система описывается следующими нечеткими прави-лами:

;

;

,

где , и  – имена входных переменных; – имя переменной вывода; , , ,,,– заданные функции принадлежности (треугольной формы).

Процедура получения логического вывода иллюстрируется рис.4.14.

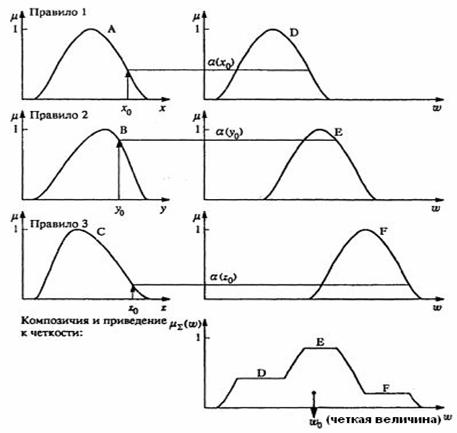
Рис. 4.14. Иллюстрация процедуры логического вывода

Предполагается, что заданы конкретные (четкие) значения входных переменных: ,  и .

На первом этапе, на основании данных значений и исходя из функций принадлежности A, B, C, находятся степени истинности ,  и  для предпосылок каждого из трех приведенных правил.

На втором этапе происходит «отсекание» функций принадлежности заключений привил (D,E,F) на уровнях , , .

На третьем этапе рассматриваются функции принадлежности, усеченные на предыдущем этапе, и производится их объединение с использованием операции max, в результате чего получается комбинированное нечеткое подмножество, описываемое функцией принадлежности  и соответствующее логическому выводу для выходной переменной .

Наконец, на четвертом этапе находится, при необходимости, четкое значение выходной переменной, например, с применением центроидного метода: четкое значение выходной переменной определяется как центр тяжести для кривой :

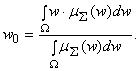
На практике используются алгоритмы вывода Mamdani, Tsukamoto, Sugeno, Larsen.

Рассмотрим наиболее употребительные модификации алгоритма нечеткого вывода, полагая, для простоты, что базу знаний организуют два нечетких правила вида:

;

,

где  и  – имена входных переменных; – имя переменной вывода; , , ,,,– некоторые заданные функции принадлежности. При этом четкое значение  необходимо определить на основе приведенной информации и четких значений  и .

Алгоритм Mamdani. Данный алгоритм соответствует рассмотренному примеру и рис.4.1. В рассматриваемой ситуации он математически может быть описан следующим образом.

1) Введение нечеткости. Находятся степени истинности для предпосылок каждого из правил , , , .

2) Логический вывод. Находятся уровни «отсечения» для предпосылок каждого из правил (с использованием операции ):

;

,

где через «» обозначена операция логического минимума ().

Затем находятся «усеченные» функции принадлежности:

;

.

3) Композиция. Производится объединение найденных усеченных функций с использованием операции , далее обозначаемой как «», что приводит к получению

итогового нечеткого подмножества для переменной вывода  с функцией принадлежности:

.

4) Приведение к четкости. Проводится для нахождения , например, центроидным методом.

Алгоритм Tsukamoto. Исходные посылки – как у предыдущего алгоритма, но здесь предполагается, что функции ,  являются монотонными.

1) Введение нечеткости – как в алгоритме Mamdani.

2) Нечеткий вывод. Сначала находятся уровни «отсечения»  и  как в алгоритме Mamdani, а затем решением уравнений:

;  

определяются четкие значения  и  для каждого исходного правила.

3) Определяется четкое значение переменной вывода (как взвешенное среднее  и ):

;

в общем случае (дискретный вариант центроидного метода):

.

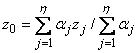Пример. Пусть заданы ; ; ; , соответствующие уровни отсечения:

,

.

и значения  и , найденные в результате решения уравнений (рис. 4.15):

 

При этом четкое значение переменной вывода:

.

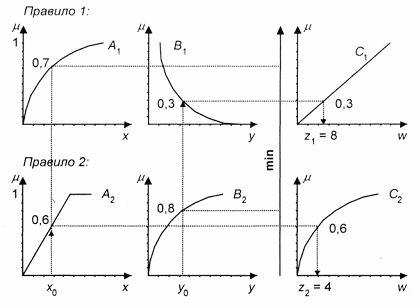
Рис. 4.15. Иллюстрация к алгоритму Tsukamoto

Алгоритм Sugeno. Sugeno и Takagi использовали набор правил в следующей форме (как и ранее, приводим пример двух правил):

;

.

Представление алгоритма (рис. 4.16).

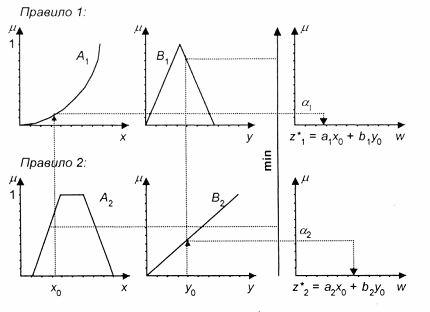
Рис. 4.16. Иллюстрация к алгоритму Sugeno

1) Введение нечеткости – как в алгоритме Mamdani.

2) Нечеткий вывод. Находятся уровни «отсечения» ,  и индивидуальные выходы правил:

;

.

3) Определяется четкое значение выходной переменной:

.

Алгоритм Larsen. В алгоритме Larsen нечеткая импликация моделируется с использованием оператора умножения.

Описание алгоритма (рис. 4.17).

1) Введение нечеткости – как в алгоритме Mamdani.

2) Нечеткий вывод. Сначала, как в алгоритме Mamdani, находятся уровни «отсечения»  и :

;

,

а затем определяются частные нечеткие подмножества:

;         .

3) Находится итоговое нечеткое подмножество:

.

В общем случае  правил:

.

4) При необходимости производится приведение к четкости, как в ранее рассмотренных алгоритмах.

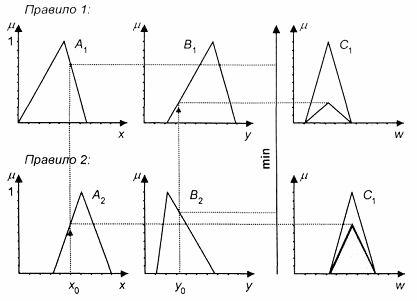
Рис. 4.17. Иллюстрация к алгоритму Larsen

Упрощенный алгоритм нечеткого вывода. Исходные правила в данном случае задаются в виде:

;                                    

,                                  

где  и – некоторые четкие числа.

Описание алгоритма (рис. 4.18).

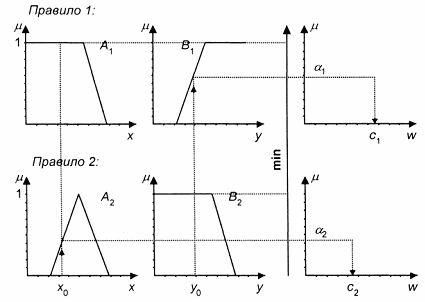
Рис. 4.18. Иллюстрация к упрощенному алгоритму нечеткого логического вывода

1) Введение нечеткости – как в алгоритме Mamdani.

2) Нечеткий вывод. Находятся уровни «отсечения»  и .

3) Определяется четкое значение выходной переменной:

,

в общем случае  правил:

.
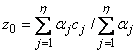