Эйлерова характеристика

Двумерной клеткой мы будем называть часть поверхности, ограниченную некоторым криволинейным многоугольником.

Теорема 1

Пусть G — граф, разбивающий замкнутую поверхность S на двумерные клетки. Пусть p — число вершин графа, q – число ребер, r – число клеток. Тогда число p – q + r не зависит от разбивающего графа и называется эйлеровой характеристикой поверхности.

Теорема 2

Пусть G — связный граф, разбивающий сферу на двумерные клетки. Тогда p – q + r = 2.

Доказательство

Примени метод индукции по q. Если q = 0, то p = 1 и r = 1. Пусть теорема верна для графа с q ребрами. Докажем ее для q + 1 ребер. Рассмотрим два случая добавления ребра (рис. 4.8). В первом случае (рис. 4.8, а) добавляется ребро, вершины не добавляются, во втором (рис. 4.8, б) добавляется ребро и вершина.

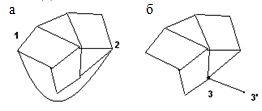
Рис. 4.8. К доказательству теоремы 2

Если обозначить новые числа вершин, ребер и граней через p’, q’, r’, то в первом случае получим:

p’ – q’ + r’ = p – (q + 1) + (r + 1) = p – q + r = 2,

во втором

p’ – q’ + r’ = (p + 1) – (q + 1) + r = p – q + r = 2.

Графы Куратовского

Далее мы рассмотрим следующие две задачи.

Первая задача принадлежит Мебиусу. Речь идет о короле, завещавшем своим пяти сыновьям разделить между собой его владения так, чтобы каждая из частей имела общие границы с каждой из остальных частей.

Рассматривая граф, вершины которого соответствуют пяти частям, а ребра – общим границам, приходим к вопросу, является ли он плоским?

Вторая задача – задача о трех домах и трех колодцах. На поверхности сферы заданы 3 точки, называющиеся домами, и 3 точки, называющиеся колодцами. Нужно соединить не пересекающимися кривыми (играющими роль тропинок) каждый дом со всеми колодцами.

Докажем неразрешимость этих двух задач.

Лемма 1

Для связного плоского графа с p > 3 вершинами и q ребрами справедливо неравенство:

q £ 3p – 6.

Если существует вложение в сферу, при котором каждая грань имеет не менее четырёх ребер, то справедливо неравенство:

q £ 2p – 4.

Доказательство

Рассмотрим множество пар (ребро, грань), где ребро содержится в грани. С одной стороны, число таких пар равно 2q, ибо каждое ребро принадлежит двум граням. С другой стороны, оно не меньше 3r, ибо грань содержит не меньше трех ребер. Отсюда:

 2q ≥ 3r. Если грань содержит не меньше четырех ребер, то получаем 2q ≥ 4r. Подставляя в эти неравенства r = 2 – p +q, получим доказываемые неравенства.

Следствие 1

Граф K₅ не плоский.

Доказательство

Граф K₅ (рис. 4.9, а) имеет  5 вершин и 10 ребер. Неравенство:

10 £ (3 ∙ 5 – 6)

неверно, значит, он не плоский.

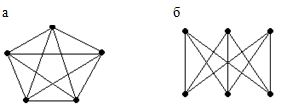
Рис. 4.9. Графы K₅  (а) и  K_3,3 (б)

Следствие 2

Граф K_3,3 не плоский.

Доказательство

В графе  K_3,3 (рис. 4.9, б) нет циклов длины 3. Отсюда в случае существования вложения в сферу каждая грань будет иметь не менее четырёх ребер. По лемме, в этом случае имеет место неравенство q £ 2p –4. Так как неравенство:

9 £ 2∙6 – 4

неверно, то граф K_3,3  не плоский.

Следовательно, обе задачи неразрешимы.

Следующая теорема Куратовского характеризует плоские графы.

Теорема 3

Граф плоский тогда и только тогда, когда он не содержит ни графа гомеоморфного K₅, ни графа гомемоморфного K_{3, 3.}

Раскраска плоского графа

Следующий вопрос – о раскраске плоских графов. В 1878 году эта проблема была поставлена Кэли на заседании Лондонского математического общества. Задана карта, состоящая из областей на сфере, которые можно интерпретировать как страны, расположенные на земной поверхности. Можно ли  произвольную такую карту раскрасить в четыре цвета так, чтобы любые две имеющие общую границу страны были окрашены в различный цвет?

Положительное решение этой проблемы было опубликовано в 1977 году Аппелем и Хакеном.

Мы докажем, что пять цветов достаточно для раскраски любой карты. Метод доказательства был предложен А.В. Кэмпе, и долгое время считалось, что этот метод годится и для четырех красок. Но это мнение было опровергнуто в 1890 году Хивудом.

Задача сводится к правильной раскраске вершин плоского графа, вершины которого соответствуют странам, а соединение вершин ребром осуществляется при наличии общей границы у стран.

Лемма 2

Пусть (V,E) – плоский конечный граф. Тогда существует вершина v Î V такая, что d(v)£ 5. Здесь d(v) – степень вершины v.

Доказательство

Иначе  2q = S d(v) ³ 6p,  и  q ³ 3p,  а мы доказали раньше, что  q £ 3p – 6.

Теорема 4

Для плоского связного графа существует правильная раскраска вершин в 5 цветов.

Доказательство

Для p £ 5 теорема верна. Пусть для p – 1 вершин теорема доказана. Рассмотрим граф с p вершинами. Найдем в нем вершину v с d(v) £ 5. Обозначим через G[v] подграф, полученный удалением вершины v и инцидентных ей ребер. Существует правильная раскраска графа G[v]. Наша задача – раскрасить вершину v.

Если d(v) < 5, то вершину v раскрасим цветом, которого нет у смежных с v вершин. Пусть d(v) = 5 и пусть все смежные с v вершины раскрашены в различные цвета. Обозначим через G₁₃ подграф (рис. 4.10) графа G[v], состоящий из вершин цвета 1 и 3. Если в нем нет путей между вершинами 1 и 3 из смежных с v, то компоненту связности вершины 3 перекрасим следующим образом: все вершины компоненты цвета 3 перекрасим в цвет 1, а все вершины компоненты цвета 1 – в цвет 3. Затем v покрасим в цвет 3.

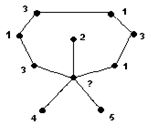
Рис. 4.10. К доказательству теоремы 4

Если в графе G₁₃ существует путь, соединяющий вершины 1 и 3 и состоящий из вершин цвета 1 или 3, то в подграфе G₂₄ нет пути между вершинами, смежными с v. В этом случае перекрасим вершины компоненты содержащей 4, аналогично тому, как это делалось выше: цвета 2 – в 4, а цвета 4 – в 2. Таким образом, если граф имеет p вершин, то для него существует правильная раскраска пятью красками. Теорема доказана.

Платоновы тела

Многогранник, у которого грани имеют одинаковое число сторон, и в каждой вершине сходится одинаковое число ребер, называется правильным. На рис. 4.11 приведены 5 правильных многогранников.

Рис. 4.11.  Пять тел Платона

Следующее приложение эйлеровой характеристики – доказательство того, что правильные многогранники исчерпываются телами Платона. По крайней мере, 5 правильных многогранников (рис. 4.11) существует.

Теорема 5

Пусть p – число вершин, q – число ребер, r – число граней правильного многогранника. Тогда возможен один из следующих случаев, рассмотренных в таблице 4.1.

Таблица 4.1 Свойства тел Платона

Многогранник	p	q	r
Тетраэдр	4	6	4
Куб	8	12	6
Октаэдр	6	12	8
Додекаэдр	20	30	12
Икосаэдр	12	30	20

Доказательство

Вершины графа, состоящего из ребер и вершин фиксированного многогранника, имеют одинаковую степень. Обозначим эту степень через x. Пусть y – число сторон грани этого многогранника. Получаем систему уравнений:

.

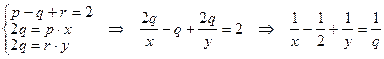Так как x, y ³ 3, а в случае x, y ³ 4 имеет место неравенство:

,

то возможны следующие случаи: x = 3  или y = 3.

Рассмотрим случай x = 3:

.

Получаем

x = 3, y = 3, ;

x = 3,  y = 4, ;

x = 3, y = 5, .

При y = 3 получаем x = 4, x = 5.

Упражнения

Свойства графов

Все графы предполагаются простыми. Графы называются изоморфными, если существует биекция f между множествами их вершин, такая что

{u,v} ребро Û {f(u), f(v)} – ребро.

1. Доказать, что граф имеет четное число вершин с нечетными степенями.

2. При встрече студентов состоялось 15 рукопожатий, три человека сделали по 4 рукопожатия, а другие – по 3. Сколько было студентов?

3. Может ли существовать группа из 23 человек, каждый из которых знаком с пятью другими?

4. В соревнованиях по шахматам по круговой системе участвуют 5 человек. Все, кроме Иванова и Петрова, сыграли различное число партий. Сколько партий сыграли Иванов и Петров?

5. Можно ли нарисовать без отрыва карандаша граф K₆, у которого удалено одно ребро?

6. Найти число попарно неизоморфных графов, у которых 2 вершины имеют степень 2, 2 вершины имеют степень 3, и 2 вершины имеют степень 4. Остальные вершины имеют степень 0.

7. Найти число попарно неизоморфных графов, у которых 3 вершины имеют степень 2, 3 вершины имеют степень 3, и 3 вершины имеют степень 4. Остальные вершины имеют степень 0.

8. Доказать, что в простом графе, имеющем не меньше двух вершин, всегда найдутся две вершины одинаковой степени.

9. Какие из графов (рис. 4.12)  изоморфны?

Рис. 4.12.  Примеры графов к вопросу 9

10. Какие из графов (рис. 4.13)  изоморфны?

Рис. 4.13. Примеры графов к вопросу 10

11. Найти число всех попарно неизоморфных графов, имеющих 4 вершины.   Нарисовать эти графы.

Рис. 4.14. Графы, имеющие 4 вершины

Ответ: существует 11 неизоморфных графов (рис. 4.14)

1. Кратчайший путь, соединяющий вершины u и  v в графе, называется геодезическим путем между вершинами. Его длина обозначается d(u,v). Диаметром  D(G) графа называется длина самого длинного геодезического пути в этом графе, т.е.

D(G)= max{d(u,v): u,v Î V}.

Найти диаметр графа, приведенного на рис. 4.15. Найти диаметр графа K₅.

Рис. 4.15. Пример графа к вопросу 12

2. Матрица смежности состоит из коэффициентов a_ij = 1 Û вершины i и j смежны:

1) построить матрицы смежности для графов K₃ и K₄;

2) доказать, что сумма коэффициентов i-й строки матрицы смежности равна степени i-й вершины;

3) построить матрицу смежности графа, состоящего из вершин и ребер куба.

4) с помощью матрицы смежности построить матрицу, коэффициентами которой является количества путей длины 2 из вершины i в вершину j.

5) объяснить, как связаны след матрицы A³ с числом треугольников в графе?

3. Циклы {z₁, z₂, …, z_n} называются независимыми, если  z₁Dz₂D … Dz_n ¹ Æ  Доказать, что у связного графа максимальное число независимых циклов равно q – p + 1.

4. Сколько компонент связности имеет лес, содержащий 76 вершин и 53 ребра?

5. Доказать, что среди 6 человек найдется тройка знакомых, или тройка незнакомых людей.

6. В компании, состоящей из пяти студентов, среди любых трех найдутся два знакомых и два незнакомых. Доказать, что компанию можно рассадить за круглым столом таким образом, что любые два соседа будут знакомы.

Хроматическое число и хроматическая функция графа

7. Вершинами графа перестановок являются перестановки n чисел {1, 2, 3, ×××, n}. Вершины, отличающиеся транспозицией, соединяются ребрами. Будет ли граф перестановок плоским при n ≥ 3? Найти хроматическое число графа перестановок чисел {1, 2, 3, …, n}.

8. Булев куб B_n размерности n состоит из вершин  (e_1, e_2, × × ×, e_n ),  e_i Î {0, 1}, где две вершины смежны, если они отличаются одной компонентой e_i . Найти хроматическое число графа B_n.

4.16. Граф A_n

1. Найти хроматическую функцию графа A_n (рис. 4.16).

2. Найти хроматическую функцию полного графа K_n.

3. Найти хроматический многочлен графа, изображением которого является буква «A».

4. Найти хроматический многочлен графа C₅.

Ответ: f(q) = q⁵ – 5q⁴ + 10q³ – 10q² + 4q.

5. Найти хроматические многочлены и хроматические числа графов (рис. 4.17).

Рис. 4.17. Примеры графов к вопросу 24

6. Соседние области флага имеют различные цвета. Сколькими способами можно раскрасить в семь цветов флаг (рис. 4.18)?

7. Соседние области флага должны иметь различные цвета. Сколькими способами можно раскрасить в q цветов флаг (рис. 4.19)?

Рис. 4.18. Пример флага к вопросу 25

Рис. 4.19. Пример флага к вопросу 26

8. Найти число раскрасок граней куба, при которых соседние грани имеют различные цвета. Число цветов не превосходит 7.

9. Построить рекуррентное соотношение для хроматических многочленов  и найти эти многочлены.

10. Найти хроматическое число графа, полученного удалением из полного графа K_n одного ребра. Двух ребер. Трех ребер, составляющих треугольник.

Ответ: n – 1, n – 1, n – 2.

Деревья

11. Является ли дерево двудольным графом?

1. Код Прюфера нумерованного дерева с n вершинами состоит из последовательности n – 2 чисел, принимающих значения от  1 до n. 

Упаковка. Код Прюфера нумерованного дерева с n вершинами строится следующим образом. В цикле находится висячая вершина с наименьшим номером. Номер вершины, смежной с найденной, записывается в последовательность. Цикл повторяется n - 2 раза.

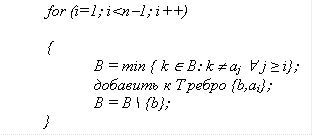Распаковка. Выписываем множество B = {1, 2, 3, …∙, n}, где n равно  длине кода плюс два. Устанавливаем начальное множество ребер дерева T = Æ. Далее выполняются действия:

Распаковать и упаковать следующие коды:

1) 4445577;

2) 24446;

3) 77321;

4) 12579213.

2. Найти число максимальных поддеревьев графа K₄.

3. Найти все максимальные поддеревья графа, полученного удалением одного ребра из графа K_4.

4.

Рис. 4.20. Максимальные поддеревья графа K₄

Ответ: см. рис. 4.20.