Напомним, что  ориентированным графом называется пара (V,A), состоящая из множества V и подмножества A Í V ´ V.  Элементы из A называются стрелками, а элементы из V – вершинами. Для стрелки (u,v) вершина u называется началом, а вершина v – концом.

Пусть (X,£) – частично упорядоченное множество. Множество

]x,y[ = {v Î X: x < v < y}

называется открытым интервалом с концами x и y.

Определение 1

Диаграммой Хассе называется ориентированный граф (V,A) с V = X и   A = {(u,v): u<v   и    ]u,v[ = Æ}.

Пример 1

На рис. 5.1 показана диаграмма Хассе множества P({0,1,2}) подмножеств множества {0,1,2}, упорядоченное отношением Í.

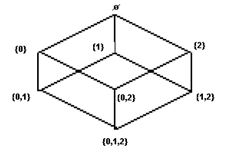
Рис. 5.1. Диаграмма Хассе множества подмножеств

Предполагается, что ребра направлены сверху вниз.

Пример 2

Для целого неотрицательного числа n³ 0 будем обозначать через [n] множество {0, 1, …∙, n}, с отношением  0 < 1< …∙ < n. Его диаграммой  Хассе  будет ориентированный граф (рис. 5.2).

Частично упорядоченные множества (X, £) и (Y, £) называются изоморфными, если существуют неубывающие отображения f: X®Y и g: Y®X, такие, что

f(g(y)) = y    и     g(f(x)) = x ("xÎX, "yÎY).

В этом случае f называется изоморфизмом, а g – обратным отображением для f.

Рассмотрим множество делителей (D_n, | ) натурального числа n³1, упорядоченное отношением делимости a | b  Û  a – делитель числа b (в этом случае говорят, что a – делит b).

Пример 3

Пусть p и q – различные простые числа, большие единицы. Диаграмма Хассе множества ( D_n, | ) с   n = p²q   показана на рисунке 5.3.

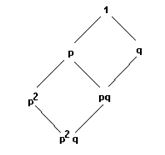
Рис. 5.3. Диаграмма Хассе множества делителей

В общем случае диаграмма Хассе частично упорядоченного множества (D_n,| ) состоит из ребер m-мерного параллелепипеда, где m – число различных простых делителей числа n.

Теорема 1

Пусть n > 0 – положительное натуральное число, n = — его разложение в произведение попарно не равных простых множителей p_i > 1. Тогда частично упорядоченное множество (D_n, |) будет изоморфно декартовому произведению линейно упорядоченных множеств:

[a₁]´ [a₂]´ … ´ [a_m].

Доказательство

Каждый делитель числа n =  будет равен числу , для некоторых 0£b₁£a₁,  0 £ b₂ £ a₂, …, 0 £ b_m £ a_m. Изоморфизм определяется как отображение, ставящее в соответствие числу  элемент (b₁, b₂, …, b_m).