Теория механизмов и машин (ТММ) является одной из важнейших научных дисциплин машиноведения. Одним из основных ее разделов является структура механизмов, в которой закладываются методологические основы всей науки о машинах и механизмах.
Известно, что основные показатели новых машин-автоматов, манипуляторов промышленных роботов и других систем закладываются на этапе выбора принципа действия, то есть на этапе структурного синтеза их кинематических схем. Благодаря работам многих отечественных и зарубежных ученых, в настоящее время созданы основные понятия и термины теории механизмов, разработана классификация механизмов, машин и их элементов. Разработаны различные методики структурного синтеза механизмов, например:
- Получить новую кинематическую схему механизма можно путем модификации существующей, заменив в ней одну или несколько кинематических пар на пары другой реализации или другого класса. Поэтому нужна была теория кинематических пар. Ее разработкой занимались многие ученые, такие как академик П.Л. Чебышев, Франц Рело, профессоры П.О. Сомов, А.П. Малышев, В.В. Добровольский, академик И.И. Артоболевский и многие другие /14/.
- Получить новую схему механизма можно также путем создания одного или нескольких исходных механизмов и присоединения к ним групп звеньев с нулевой степенью подвижности (групп Ассура).
- Получить новую схему механизма можно также, если задать в пространстве положения направляющих или осей вращения входных и выходных звеньев, а затем сконструировать кинематическую цепь, соединяющую эти звенья.
При обобщении этих методов структурного синтеза нами приняты следующие основные положения:
- определения и термины, как правило, соответствуют общепринятым;
- механизм считается образованным из кинематической цепи путем задания стойки, входных и выходных звеньев;
- рассматриваются, как правило, кинематические цепи с замкнутыми независимыми контурами;
- используется классификация кинематических пар по числу накладываемых парой связей;
- звенья считаются идеальными, кинематические пары используются без пассивных связей и избыточных степеней свободы, не участвующие в преобразовании движения и ввести которые можно после выполнения структурного синтеза;
- подвижность цепей определяется известной формулой Сомова-Малышева.
При разработке одной из подсистем САПР ММ – АРМ структурного синтеза механизмов машин, в памяти ЭВМ можно было бы записать банк данных (БнД), охватывающий огромное количество различных, теоретически пригодных к использованию
кинематических схем механизмов (КСМ), большая часть которых описана в известном справочнике механизмов И.И. Артоболевского. Затем, по сформулированным критериям отбора, программным путем можно было бы просмотреть весь банк данных и отобрать необходимые схемы.
Однако банк данных не может содержать информацию обо всех существующих механизмах в связи с их огромным количеством. Поэтому он должен быть сформирован из таких носителей минимальной информации о структуре, из которых можно получить любую схему механизма программным путем.
Проиллюстрируем свойства КСМ на примере кулисно-рычажного механизма 1001 /4/ (рис.5.1). Она имеет:
- число звеньев (n=6);
- число кинематических пар (m=7). Целесообразно кинематические пары обозначать через номера их звеньев, см. табл. 5.1; в ней В – вращательная пара, П – поступательная пара;
- число контуров (к=2);
- последовательность соединения звеньев в каждом контуре:
1-й контур (1,2,3,4), 2-й контур (1,4,5,6);
- подвижность механизма (W=1), определяемая по формуле Сомова-Малышева:
(5.1)
где Рj – количество пар j-го класса, j-класс по классификации Артоболевского. Pj=7;
- число общих ограничений, накладываемых кинематическими парами, по классификации В.В. Добровольского (ν=3);
- многопарность звеньев. Для схемы, показанной на рис. 5.1, имеем SP1=0; SP2=4; SP3=2; SP4=0…, причем 
, где SPi – число звеньев имеющих i - кинематических пар;
- метрика механизма, то есть размеры его звеньев;
- стойка (звено 1); обобщенные координаты: входное звено — 2, выходные — 4, 6 (рис. 5.1).
 |
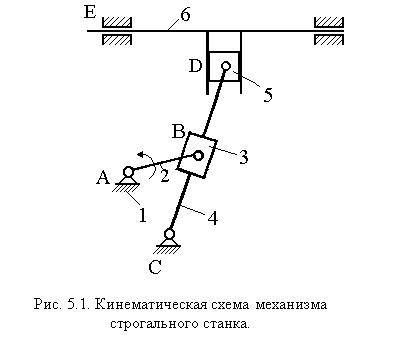Таблица 5.1
Кинематические пары и их обозначение
|
Обозначение пары |
Кинематическая пара |
||
|
Принято |
Через номера звеньев |
Класс |
Тип |
|
A |
1 – 2 |
5 |
В |
|
B |
2 – 3 |
5 |
В |
|
B |
3 – 4 |
5 |
П |
|
C |
4 – 1 |
5 |
В |
|
D |
4 – 5 |
5 |
В |
|
D |
5 – 6 |
5 |
П |
|
E |
6 – 1 |
5 |
П |
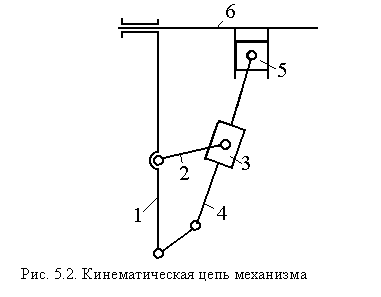
С кинематической схемой механизма тесно связано понятие кинематической цепи (КЦ). Кинематическая цепь (рис. 5.2) – это система звеньев, связанных между собой кинематическими парами. Звенья цепи могут быть полуповодковыми (однопарными), (например, свободно вращающийся шкив, ротор, педаль велосипеда, захват робота), поводковыми (двупарными), последовательное соединение которых образует двуповодковые цепочки (рис. 5.2, звенья 2 — 3 и 5 — 6), и многопарными, имеющими более двух кинематических пар (рис. 5.2, звенья 1 и 3).
В дальнейшем, будем рассматривать только кинематические цепи, имеющие один или несколько замкнутых контуров.
Известно, чтобы получить механизм из КЦ, необходимо в ней выбрать стойку, подсчитать подвижность (W), назначить входные, выходные звенья и задать метрику (схема на рис. 5.1 получена из КЦ на рис. 5.2). Остальные свойства КЦ наследует от КСМ (вернее, наоборот).
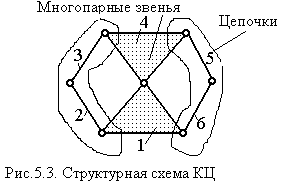
Поэтому задача структурного синтеза механизмов сводится к аналогичной задаче синтеза кинематических цепей. КЦ тесно связана с понятием структурная схема (ССКЦ). Структурная схема КЦ (рис. 5.3) имеет часть свойств КСМ:
- число звеньев (n=6);
- число кинетических пар (m=7) без указания их классов;
- число контуров (k=2);
- последовательность соединения звеньев: 1-2-3-4, 1-4-5-6;
- многопарность звеньев SPi, i=1… imax;
В структурной схеме можно выделить двуповодковые цепочки (для рассматриваемого примера их две (2-3), (5-6)).
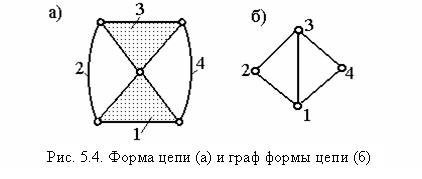
Упрощенное изображение замкнутой кинематической цепи, состоящей из многопарных звеньев и двуповодковых цепочек, последовательно соединенных кинематическими парами, назовем формой цепи (рис.5.4).
Форма цепи (ФЦ) инвариантна относительно плоскостей движения звеньев (то есть плоские и пространственные кинематические цепи имеют одну и ту же форму цепи), классов кинематических пар, числа двупарных звеньев в двуповодковых цепочках, подвижности кинематической цепи (из одной формы цепи можно получить механизм любой подвижности). Звенья и цепочки в форме цепи перенумеруем цифрами 1,2,…,n.
ФЦ несет в себе минимальную информацию о структурной схеме:
- число звеньев с учетом числа двуповодковых цепочек (nф=4);
- число кинематических пар (mф=6);
- многопарность (SP2=2, SP3=2);
- число контуров (k=2);
- последовательность соединения цепочек с многопарными звеньями (1-2-3, 1-3-4).
В связи с этим, ее можно использовать, как исходный объект структурного синтеза, несущий в себе минимальное количество информации схемы механизма.
 |
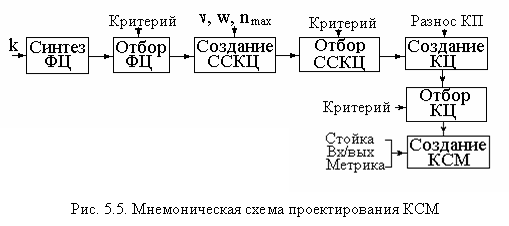
На основе понятия ФЦ может быть разработана методология структурного синтеза механизмов машин, выполняемая в соответствии с мнемонической схемой (рис. 5.5):
O синтез форм цепей (ФЦ);
O отбор форм цепей в соответствии с заданными критериями;
O создание структурной схемы кинематической цепи (ССКЦ);
O отбор ССКЦ по заданным критериям;
O создание кинематической цепи (КЦ);
O отбор КЦ по заданным критериям;
Oсоздание кинематической схемы механизма (КСМ).
Рассмотрим более подробно только первый этап. Синтез ФЦ начинается с расчета возможных сочетаний многопарных звеньев.
Пусть: k — число контуров ФЦ;
i — многопарность звена ФЦ;
SPi - число звеньев, имеющих i – кинематических пар;
imax - максимальное число элементов кинематических пар на одном звене;
nф — общее число звеньев ФЦ (включая двуповодковые цепочки);
mф – общее число кинематических пар ФЦ.
Тогда для разработки математической модели расчета возможных сочетаний многопарных звеньев используем следующие инварианты:
- связь числа контуров, пар и звеньев:
mф=nф + k – 1; (5.2)
- общее число звеньев, равное сумме многопарных и двупарных звеньев (цепочек):
; (5.3)
- удвоенное число кинематических пар, равное сумме всех многопарных и двупарных звеньев (цепочек):
. (5.4)
Подставим (5.3) и (5.4) в (5.2) и получим:
. (5.5)
Анализ формулы (5.5) показал, что imax=2∙(k-1)+2=2k, тогда расчет возможных сочетаний многопарных звеньев ФЦ можно выполнить по формуле (5.6)
. (5.6)
Расчет можно выполнить по следующему алгоритму. Задается значение k и формируется массив р с числом элементов, равным 2×k. Объявляется бесконечный цикл, выход из которого выполняется по условию
p3 = 1 & p2×k = 1.
В теле бесконечного цикла инкрементируется p3, затем создается внутренний цикл 3 £ i £ 2×k, проверяющий условие: если pi больше предельно допустимого значения, определяемого из тождества (5.6), то pi очищается, а pi+1 инкрементируется. Далее проверяется тождество (5.6); если оно выполняется, то массив копируется, как строка, в возвращаемую матрицу Р. Создается матрица многопарных звеньев, как, например, матрица D (в ней первый столбец – число контуров, второй – число кинематических пар многопарных звеньев, остальные указывают число многопарных звеньев SPi):
Отбор возможных сочетаний многопарных звеньев ФЦ осуществляется с помощью критериев, ограничивающих их многопарность: SPi £ <число>, где <число> — значение, устанавливаемое пользователем (по умолчанию для заданного SPi оно принимается максимальным). Таким образом, созданные программным путем матрицы (D) состава SPi многопарных звеньев для k = 2 ¸ 6 можно рассматривать как исходные, используемые для дальнейшего проектирования форм цепей.
Синтез форм цепей на основе теории графов можно выполнить по следующему алгоритму. Пусть имеется В многопарных звеньев SPi ФЦ, где i >2 (столбец D). Например, для набора SP3 = 2, SP4 = 1 (вторая строка D) их вид показан на рис. 5.6, а. Пронумеруем их вершины цифрами 1,2,…,n и составим списки элементов вершин В:
В1=(1,2,3,4); В2=(5,6,7); В3=(8,9,10). В зависимости от порядка соединения вершин элементов Вi, конструкции графов будут различны.
Пусть Г — множество графов, полученных в результате изменения порядка соединения дугами вершин всех элементов Вi. Такое изменение будем выполнять с исходного графа, которым может быть любой, например Г1, у которого вершины соединены попарно, в порядке возрастания их номеров:
Г1=(1,2)(3,4)(5,6)(7,8)(9,10).
На рис. 5.6, б показан исходный граф, его форма цепи распадается на две самостоятельные схемы. При изменении порядка соединения вершин графа могут получиться структурно-различные формы цепи, такие как, например,
Г2=(1,2)(3,5)(4,6)(7,8)(9,10),
контуры которого соединяются последовательно (рис. 5.6, в), но их можно разъединить, разрезав поводок 7 – 8 и четырехпарное звено, тем самым получить самостоятельные конструкции. Наконец, в графе
Г3=(1,9)(2,10)(3,5)(4,6)(7,8)
контуры являются смежными (рис. 5.6, г) и ФЦ разделить на простейшие конструкции не удается. Именно такие ФЦ представляют для нас наибольший интерес.
Алгоритм создания множества Г заключается в следующем:
Из матрицы D выбираются возможные сочетания многопарных звеньев ФЦ Вi и изображаются в виде многоугольников. Каждая вершина Вi кодируется двумя цифрами: первая указывает номер элемента Вi, вторая – номер вершины в элементе Вi. Вершины многопарных звеньев нумеруются в любой последовательности. Формируется матрица А (из двух строк и n столбцов), содержащая списки номеров вершин элементов Вi. Записывается исходный граф Гi в виде списка, в котором каждая вершина j-го столбца первой строки предполагается соединенной с соответствующей вершиной второй строки. С помощью циклов for можно изменить порядок соединения некоторых ребер графа Гi-1 и записать новый граф Гi в виде нового списка. После окончания циклов for из множества Г должны быть исключены дублируемые (изоморфные) графы.