Как и обычный метод Z-преобразования, метод дробного квантования не позволяет найти непрерывный сигнал , а лишь дает возможность определить соответствующую ему решетчатую функцию. Но дискреты этой функции разделены интервалами времени, равными  (где N – целое число), т.е. расположены в N раз чаще по сравнению с дискретной функцией .

Обозначим такую решетчатую функцию , а соответствующее ей Z-изображение – . Согласно методу дробного квантования указанное Z-изображение равно:

                                       (5.1)

где  может быть получена из обычной передаточной функции системы заменой в последней z на , и  на . Величина N определяется числом требуемых дополнительных значений . Если внутри интервала квантования требуется R дополнительных точек, то .

Пример 24

Воспользуемся исходными данными примера 17 и определим два дополнительных значения внутри интервала квантования для решетчатой переходной функции.

Поскольку , то . Передаточная функция дробного квантования, полученная по (см. пример 17):

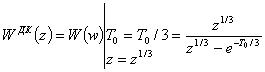
Z-изображение переходной функции в соответствии с выражением (5.1) имеет вид:

Дробная степень z в последнем выражении затрудняет дальнейшие преобразования, поэтому можно ввести в рассмотрение новую переменную , тогда получим:

Разлагая  в ряд Лорана, получим:

Следовательно:

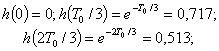
 и т.д.

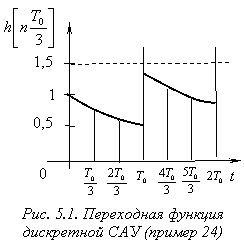
График функции h(t) имеет вид (рис. 5.1):

Следовательно, график функции , построенный по значениям дискрет функции , (см. рис. 2.10) неверен. В этом легко убедиться и без применения дробного квантования, достаточно воспользоваться формулой (1.10). Но при определении вида непрерывных сигналов в более сложных дискретных системах возможность получения дополнительных дискрет внутри интервала квантования является несомненным достоинством рассмотренного метода.