Примером резьбовых соединений с предварительной затяжкой, нагруженных внешней осевой силой, служит крепление крышки резервуара, находящегося под давлением (р) жидкости или газа (рис. 5.16). Полная сила, растягивающая болты (винты) при действии расчетного давления (р), Н/мм², складывается из силы давления среды на крышку и остаточной силы, потребной для сжатия прокладки:

,

,    (5.17)

где R – полная сила, растягивающая болты, Н/мм²; р  – расчетное давление, Н/мм2; ψ – коэффициент, учитывающий возможное повышение давления (обычно );  и  – соответственно наружный и внутренний (в данном случае равен внутреннему диаметру резервуара) диаметры прокладки, мм;  – давление на прокладке, Н/мм², принимаемое для мягких прокладок равным , а для металлических прокладок – ;  – внешняя осевая сила, приходящаяся на один болт, Н;  – число болтов.

Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой.

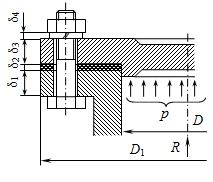
Рис. 5.16. Соединение, нагруженное силой, нарушающей герметичность соединения

После приложения внешней нагрузки (F), приходящейся на один болт, к затянутому соединению болт дополнительно растянется на некоторую величину , а деформация сжатия деталей уменьшится на ту же величину. Для простоты можно считать, что часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку (раскрытие) стыка. Тогда дополнительная нагрузка болта равна  ( – коэффициент внешней нагрузки, учитывающий приращение нагрузки болта), а уменьшение затяжки стыка равно .

Значение коэффициента  определяют из условия совместности деформаций (т.е. по условию равенства дополнительных деформаций болта и деталей):

,                                              (5.18)

где  – коэффициент податливости болта, мм/Н;  – суммарный коэффициент податливости соединяемых деталей, мм/Н.

Из равенства (5.18) имеем:

.

Коэффициент податливости равен:

· для болтов постоянного сечения

,

· для болтов переменного сечения

,

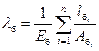где  – длина болта, мм;  – модуль продольной упругости материала болта, Н/мм²;  – площадь поперечного сечения болта, мм²; – длина -го участка болта, мм;  – площадь поперечного сечения -го участка болта, мм².

Суммарный коэффициент податливости деталей определяется следующим образом:

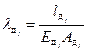,       , (5.19)

где  – коэффициент податливости -й детали, мм/Н;  – толщина -й детали, мм;  – модуль продольной упругости материала -й детали, Н/мм²;  – расчетная площадь поперечного сечения -й детали, мм².

В формуле (5.19) под расчетной площадью  понимают площадь только той части детали, которая участвует в деформации от затяжки болта. Полагают, что деформации от гайки и головки болта распространяются в глубь деталей по конусам (рис.5.17) с углом  (). Объемы этих конусов приравнивают к объему цилиндра с диаметром:

.

Тогда расчетная площадь будет определяться по формуле:

.

Из условия сохранения плотности стыка сила предварительной затяжки равна:

,

где  – коэффициент затяжки.

Рис. 5.17. К определению расчетной площади болта

Коэффициент затяжки принимается равным:

1) по условию нераскрытия стыка:

· при постоянной нагрузке ;

· при переменной нагрузке .

2) по условию герметичности соединения:

· при мягкой прокладке ;

· при металлической фасонной прокладке ;

· при металлической плоской прокладке .

Расчетная осевая сила (), действующая на затянутый болт, после приложения внешней нагрузки () с учётом формулы (5.17) будет определяться следующим образом:

.  (5.20)

При приближенных расчетах для соединений из стальных деталей без мягкой прокладки .

Предварительно определив значение расчетной осевой силы по формуле (5.20), затем при статической нагрузке определяют внутренний диаметр резьбы () по формуле (5.11). По найденному значению  подбирают стандартный болт (винт).

Примечание: Правильнее крутящий момент затяжки учитывать при определении расчетной осевой силы  (поскольку внешняя осевая сила не создает момента затяжки):

,

далее определяют внутренний диаметр резьбы  не по формуле (5.11), а по формуле (5.10), при этом в данную формулу вместо осевой силы F необходимо подставить найденное значение расчетной осевой силы .

При переменной нагрузке определяется коэффициент запаса прочности

,   (5.21)

где  – предел выносливости материала болта при симметричном цикле изменения напряжений, МПа;  – амплитуда цикла напряжений, МПа;  – коэффициент чувствительности к асимметрии цикла напряжений;  – постоянная составляющая цикла напряжений, МПа;  – эффективный коэффициент

концентрации напряжений (для углеродистых сталей , для легированных сталей  – большие значения принимаются при диаметре болта мм).