Случай, когда нагрузка соединения раскрывает стык деталей, часто встречается на практике (крепление кронштейнов, стоек и т.п.). Расчет соединения рассмотрим на примере (рис. 5.20).
Внешнюю нагрузку (
) раскладываем на составляющие 
и 
. Составляющие внешней нагрузки переносим в центр стыка, при этом необходимо добавить момент (
):
.
Момент () и сила 
раскрывают стык, а и сила 
сдвигает детали в плоскости стыка. Устранение раскрытия стыка и сдвига деталей обеспечивается затяжкой болтов с силой 
.
Расчет соединения по условию нераскрытия стыка
Сила затяжки образует в стыке напряжения смятия, равномерно распределенные по поверхности стыка (рис. 5.20):
, (5.22)
где 
– напряжение смятия, МПа 
– число болтов; 
– площадь стыка, мм2.
Сила растягивает болты и уменьшает напряжение на величину (см. подразд. 5.10):
.
На практике в подобных соединениях значения коэффициента внешней нагрузки (
) мало, поэтому приближенно можно считать, что
.
При 
увеличивается запас по условию нераскрытия стыка.
Применяя принцип наименьшего сопротивления, можно считать, что поворот кронштейна происходит вокруг оси симметрии стыка. Это условие соблюдается при большой затяжке болтов, обеспечивающей нераскрытие стыка. При раскрытии стыка ось поворота смещается от оси симметрии к кромке стыка. При отсутствии затяжки осью поворота является кромка стыка. До тех пор, пока стык не раскрылся, кронштейн и основание можно рассматривать как единое целое.
Напряжения в стыке (
) от действия момента (
) распределяются аналогично нормальным напряжениям при деформации изгиба. Пренебрегая значением 
, приближенно получим:
,
где 
– осевой момент сопротивления изгибу, определяемый для площади стыка, мм3.
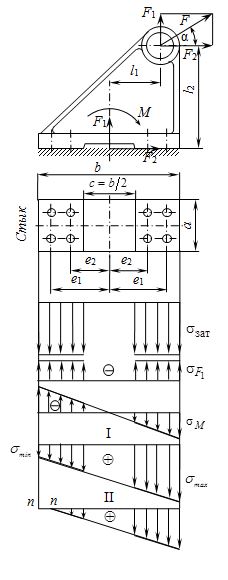
Рис. 5.20. Нагрузка соединения, раскрывающая стык
Для сплошной поверхности стыка (первый случай)
; 
.
Для поверхности стыка в рассматриваемом примере (см. рис. 5.20) площадь стыка равна (второй случай):
; 
.
При одинаковой внешней нагрузке 
напряжение 
во втором случае возрастает на 12 % по сравнению со сплошной поверхностью стыка, а площадь стыка уменьшается на 50 %. Тогда условие нераскрытия стыка во втором случае обеспечивается затяжкой болтов на 38 % меньше по сравнению с первым случаем.
В зависимости от силы затяжки и внешней нагрузки возможны два варианта распределения суммарных напряжений по поверхности стыка. Максимальное 
и минимальное 
напряжения в стыке определяются по формулам:
; 
.
В приведенных формулах за положительное принято напряжение смятия (затяжки) 
.
Вариант II (см. рис. 5.20) свидетельствует о раскрытии стыка на участке 
, так как суммарное напряжение здесь равно нулю, что является недопустимым.
Вариант I свидетельствует о нераскрытии стыка и рассматривается как расчетный. По условию нераскрытия стыка
,
или
,
или
, (5.23)
где 
– коэффициент запаса по нераскрытию стыка; верхний знак «–» перед напряжением 
берется при направлении составляющей 
(см. рис. 5.20) к стыку соединяемых деталей; нижний знак «+» – от стыка.
По формуле (5.23) определяют значение 
, а затем по формуле (5.22) находят необходимую силу затяжки 
.
Расчет соединения по условию отсутствия сдвига деталей
При отсутствии разгрузочного устройства от сдвига деталей сила 
должна уравновешиваться силами трения в стыке при постановке болтов в отверстия с зазором:
, (5.24)
где 
– сила затяжки, найденная по формуле (5.22); 
– коэффициент трения в стыке; 
– коэффициент запаса по отсутствую сдвига деталей.
Ориентировочно можно принять: 
– сталь (чугун) по бетону; 
сталь (чугун) по дереву; 
– сталь по чугуну (по стали).
В формуле (5.24) не учитывается момент (), так как он не сдвигает детали и не меняет суммарного значения сил трения в стыке. Если условие (5.24) не выполняется, то условие (5.23) не является решающим, и силу затяжки следует определять исходя из условия (5.24) по формуле:
(5.25)
или следует устанавливать болты в отверстия без зазора.